Short Answer Type
of the corresponding sides of the first triangle.
of the corresponding sides of the first triangle.
times the corres ponding sides of the isosceles triangle.
of the corresponding sides of the triangle ABC.
Long Answer Type
times the corresponding sides of the given triangle.
Short Answer TypeSteps of Construction :
(i) Bisect PQ. Let M be the mid-point of PO.
(ii) Taking M as centre and MO as radius, draw a circle which intersect the given circle at the points A and B.
(iii) Join PA and PB.
Now, PA and PB are the required two tangents.
(iv) Bisect QO. Let N be the mid-point of QO.
(v) Taking N as centre and NO as radius, draw a circle. Let it intersect the given circle at the points C and D.
(vi) Join QC and QD.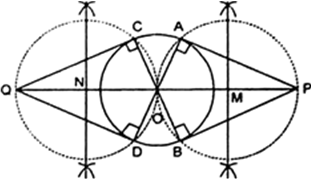
Then QC and QD are the required two tangents.
Justification : Join OA and OB.
Then ∠PAO is an angle in the semicircle and, therefore,
∠PAO = 90°
⇒ PA ⊥ OA
Since, OA is a radius of the given circle, PA has to be a tangent to the circle. Similarly, PB is also a tangent to the circle.
Again, Join OC and OD.
Then ∠QCO is an angle on the semicircle and therefore,
∠QCO = 90°
Since, OC is a radius of the given circle, QC has to be a tangent to the circle.
Similarly, QD is also a tangent to the circle.
Switch
