Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

81. Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.

581 Views

82. Let ABC be a right angle in which AB = 6 cm, BC = 8 cm and ∠B = 90°. BD is the perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.

1351 Views

83. Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.

602 Views

84. Draw a line segment of length 7.6 cm and divide it in the ratio 3 : 5.

648 Views

85. Divide the given line segment AB of length 6 cm internally in the ratio 3 : 4.

930 Views

Long Answer Type

86. Divide a line segment 11 cm in the ratio of 2 : 5 (a) internally (b) externally.

(a) Internally : Steps of Construction :

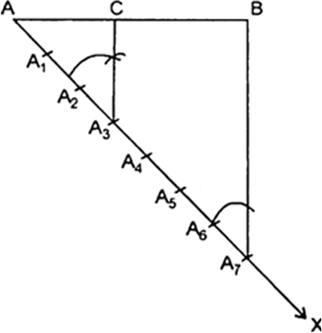
(i)    Draw AB =11 cm.
(ii)    Draw a ray AX making an acute ∠ BAX.
(iii)    Along AX, mark points A₁, A₂, A₃ .........,
A₇. Such that AA_l = A₁A₂ = .......= A₆A₇.
(iv)    Join A₇ B.
(v) Through A₂, draw a line A₂C || A₇B intersecting AB at C.
Thus, point C so obtained is the required point which divides AB internally in the ratio 2
: 5.
(b) Externally : Steps of Construction
(i)    Draw AB = 11 cm.
(ii)    Draw a ray BX making an acute ∠ ABX.
(iii)    Along a ray BX, mark points B₁, B₂,..., B₅, such that BB₁ = B₁B₂ = B₂B₃ =
B₃B₄= B₄B₅.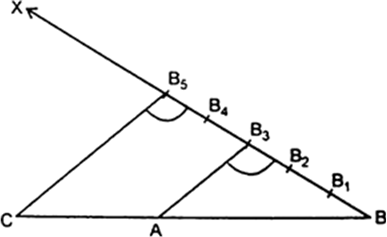

(a) Internally : Steps of Construction :
(i) Draw AB =11 cm.(ii

(iv) Join B₃A.
(v) Through B₅, draw a line parallel to B₃A intersecting BA produced at C.
Thus, point C so obtained is the required point which divides AB externally in the ratio 2 : 5.
Constructions Based on similar triangle

733 Views

Short Answer Type

87. Construct a triangle ABC in which AB = 5 cm, ∠B = 60° and altitude CD = 3 cm. Construct a triangle AQR similar to ΔABC, such that each side of ΔAQR is 1.5 times that of the corresponding side of ΔABC.

2143 Views

88. Construct a ΔPBC, similar to a given ΔPQR, with QR = 6 cm, PR = PQ = 5 cm, such that each of its side is 5/7th of the corresponding sides of the ΔPQR.

224 Views

89. Draw a ΔABC in which BC = 6 cm, AB = 4 cm and AC = 5 cm. Draw a triangle similar to ΔABC with its sides equal to 3/4th of the corresponding sides of ΔABC.

749 Views

90. Construct a ΔABC in which BC = 6 cm, m∠BAC = 60° and median through A is 4.5 cm. Construct a ΔA ‘BC’ similar to ΔABC with BC’ = 8 cm.

168 Views