Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Constructions

Short Answer Type

151. Divide a line segment of 7 cm internally in the ratio 2 : 3

1527 Views

152. Draw a circle of radius 3 cm. From a point 5 cm away from the centre of the circle, draw two tangents to the circle. Find the length of the tangents.

87 Views

153. Construct a ΔABC in which AB = 6.5 cm, ∠B = 60° and BC = 5.5 cm. Also, construct a triangle ABC similar to ΔABC, whose each sice

3 over 2

times the corresponding side of the ΔABC.

127 Views

154.

Construct a ΔABC in which AB = 6.5 cm, ∠B = 60° and BC = 5.5 cm. Also, construct a triangle ABC similar to ΔABC, whose each side $bold 3 over bold 2$ times the corresponding side of the ΔABC.

124 Views

155. Draw a ΔABC with sides BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Construct a ΔABC similar to ΔABC, such that sides of ΔABC are

bold 3 over bold 4

of the corresponding sides of ΔABC.

101 Views

156. Draw a circle of radius 4 cm. Form a point P, 7 cm from the centre of the circle, draw a pair of tangents to the circle. Measure the length of each tangent segment.

149 Views

157. Draw a right triangle in which the sides containing the right angles are 5 cm and 4 cm. Construct a similar triangle whose sides are

bold 5 over bold 3

times the sides of above.

196 Views

158.

Draw a circle of radius 4 cm. Draw two tangents to the circle inclined at an angle of 60^o to each other.

4680 Views

Long Answer Type

159.
Prove that the length of tangents drawn from an external point to a circle is equal.

Given: TP and TQ are two tangent drawn from an external point T to the circle C (O, r).

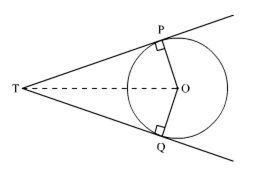
To prove: TP = TQ

Construction: Join OT

Proof: we know that a tangent to the circle is perpendicular to the radius through the point of contanct.

∴ ∠OPT = ∠OQT = 90^o

In Δ OPT and ΔOQT

OT = OT (common)

OP = OQ (radius of the circle)

∠OPT = ∠OQT (90^o)

∴ ∠OPT = ∠OQT (RHS congruence criterion)

⇒ TP = TQ (CPCT)

Hence, the length of the tangents drawn from an external point to a circle is equal.