Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Constructions

Short Answer Type

161.

Draw a line segment of length 8 cm and divide it internally in the ratio 4: 5.
Steps of construction.

5037 Views

Long Answer Type

162.
Construct an isosceles triangle with base 8 cm and altitude 4 cm. Construct another triangle whose sides are 2/3 times the corresponding sides of the isosceles triangle.

Steps of Construction

Step 1. Draw a line segment BC = 8 cm.

Step 2. Draw the perpendicular bisector XY of BC, cutting BC at D.

Step 3. With D as centre and radius 4 cm, draw an arc cutting XY at A.

Step 4. Join AB and AC. Here, ∆ABC is isosceles whose base is 8 cm and the altitude is 4 cm.

Step 5. Below BC, draw an acute angle ∠CBX.

Step 6. Along BX, mark three points B₁, B₂ and B₃ such that BB₁ = B₁B₂ = B₂B₃.

Step 7. Join CB3.

Step 8. From B2, draw B2C' || CB₃ meeting BC at C'.

Step 9. From C', draw A'C' || AC meeting AB in A'.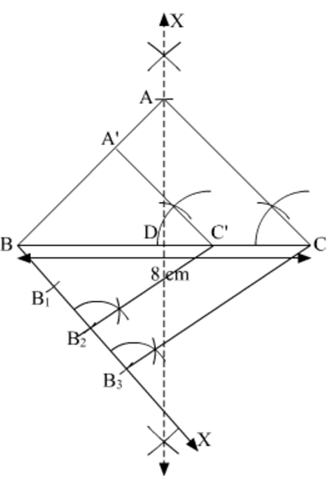

9502 Views

163.

Draw a triangle ABC with BC = 6 cm, AB = 5 cm and ∠ABC 60. Then construct a triangle whose sides are 3/4 of the corresponding sides of the △ABC.

164.

Construct a tangent of a circle of radius 4 cm from a point on the concentriccircle of radius 6 cm.

165.

Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.

166.

Construct a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then construct another triangle whose sides are 3/4 times the corresponding sides of the Δ ABC.

167.

Draw a triangle ABC with side BC = 6 cm, $∠$ C = 30⁰ and $∠$ A = 105⁰. Then construct another triangle whose sides are $\frac{2}{3}$ times the corresponding sides of $∆$ ABC.