7.

Construct the following angles and verify by measuring them by a protractor:

105°

105°
Given: A ray OA.
Required: To construct an angle of 105° at O.
Steps of Construction:
1. Taking O as centre and some radius, draw an arc of a circle, which intersects OA, say at a point B.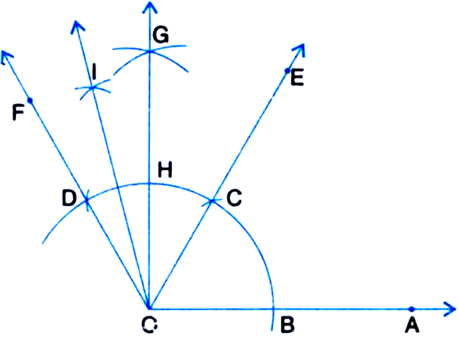



2. Taking B as centre and with the same radius as before, draw an are intersecting the previously drawn arc, say at a point C.
3. Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.
4. Draw the ray OE passing through C. Then ∠EOA = 60°.
5. Draw the ray OF passing through D. Then ∠FOE = 60°.
6. Next, taking C and D as centres and with the radius more than  CD, draw arcs to intersect each other, say at G.
7. Draw the ray OG intersecting the arc drawn in step 1 at H. This ray OG is the bisector of the angle FOE,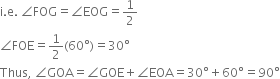 


8. Next, taking H and D as centres and with the radius more than  HD, draw arcs to intersect each other, say at I. 9. Draw the ray OI. This ray OI is the bisector of the angle FOG,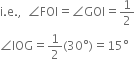 



Thus, ∠IOA = ∠IOG + ∠GOA = 15° + 90° = 105°. On measuring the ∠IOA by protractor, we find that ∠IOA = 105°.
Thus, the construction is verified.