8.

Construct the following angles and verify by measuring them by a protractor:

135°

135°

Given: A ray OA.
Required: To construct an angle of 135° at O. Steps of Construction:
1. Produce AO to A' to form ray OA'.
2. Taking O as centre and some radius, draw an arc of a circle, which intersects OA at a point B and OA' at a point B'.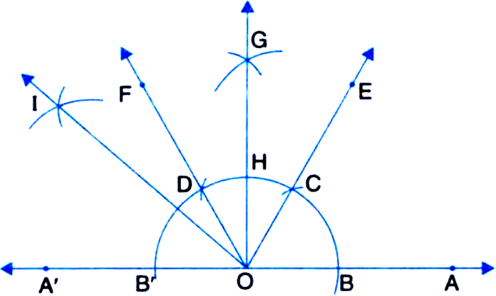

3. Taking B as centre and with the same radius as before, draw an arc intersecting the previously drawn arc at a point C.
4. Taking C as centre and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.
5. Draw the ray OE passing through C.
Then ∠EOA = 60°.
6. Draw the ray OF passing through D.
Then ∠FOE = 60°.
7. Next, taking C and D as centres and with the radius more than CD, draw arcs to intersect each other, say at G.
8. Draw the ray OG intersecting the arc drawn in step 1 at H. This ray OG is the bisector of the angle FOE,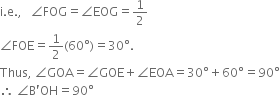 

9. Next, taking B' and H as centres and with the radius more than the radius more than  B'H, draw arcs to intersect each other, say at I.

10. Draw the ray OI. This ray 01 is the bisector of the angle B'OG, i.e., ∠B'OI = ∠GOI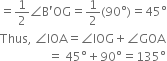

On measuring the ∠IOA by protractor, we find that ∠IOA = 135°.
Thus, the construction is verified.