Short Answer TypeConstruct a triangle XYZ in which ∠Y = 30°, ∠Z = 90° and XY + YZ + ZX = 11 cm.
Given: In triangle XYZ, ∠Y = 30°, ∠Z = 90° and XY + YZ + ZX = 11 cm.
Required: To construct the ∆XYZ.
Steps of Construction:
1. Draw a line segment BC = XY + YZ + ZX (= 11 cm).
2. Make ∠LBC = ∠Y (= 30°) and ∠MCB = ∠Z (= 90°).
3. Bisect ∠LBC and ∠MCB. Let these bisectors meet at a point X.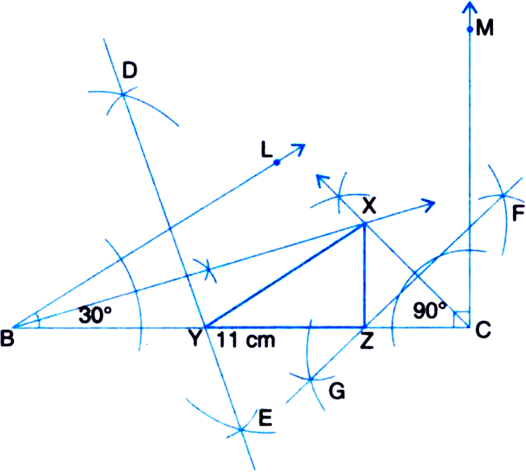
4. Draw perpendicular bisectors DE of XB and FG of XC.
5. Let DE intersect BC at Y and FG intersect BC at Z.
6. Join XY and XZ.
Then, XYZ is the required triangle.
Switch
