Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Continuity and Differentiability

Short Answer Type

1. Check the continuity of the function f given by f(x) = 2 x + 3 at x = 1.

332 Views

Long Answer Type

2. Prove that the function f(x) = 5 x – 3 is continuous at x = 0, at x = – 3 and at x = 5.

424 Views

Short Answer Type

3. Examine the continuity of the function f(x) = 2x² –1 at.x = 3

137 Views

4. Prove that the function f(x) = xⁿ is continuous at x = n, where n is a positive integer.

132 Views

5. Examine whether the function f given by f(x) = x² is continuous at x = 0.

147 Views

6. Is the function defined by f(x) = x² –sin x + 5 continuous at x =

98 Views

Discuss the continuity of the function f given by f(x) = | x | at x = 0.

124 Views

8. Prove that the identity function on real numbers given by f(x) = x is continuous at every real number.

138 Views

9. Show that the function defined by g(x) = x – [x] is discontinuous at all integral points. Here [x] denotes the greatest integer less than or equal to x

85 Views

10. Find all the points of discontinuity of the greatest integer function defined by f(x) = [x], where [x] denotes the greatest integer less than or equal to x.

Let f(x) = [ x ]. D_f = R
Let a be any real number ∈ D_f.
Two cases arise:
Case I. If a is not an integer, then
$Lt with straight x rightwards arrow straight a below space straight f left parenthesis straight x right parenthesis equals space Lt with straight x rightwards arrow straight a below space left square bracket straight x right square bracket equals left square bracket straight a right square bracket equals straight f left parenthesis straight a right parenthesis$
⇒ f is continuous at x = a

Case II. If a ∈ 1, then f(a) = [ a ] = a and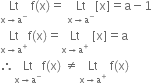
$Lt with straight x rightwards arrow straight a to the power of minus below space straight f left parenthesis straight x right parenthesis equals space Lt with straight x rightwards arrow straight a to the power of minus below left square bracket straight x right square bracket equals straight a minus 1 Lt with straight x rightwards arrow straight a to the power of plus below straight f left parenthesis straight x right parenthesis equals Lt with straight x rightwards arrow straight a to the power of plus below space left square bracket straight x right square bracket equals straight a therefore Lt with straight x rightwards arrow straight a to the power of minus below straight f left parenthesis straight x right parenthesis space not equal to Lt with straight x rightwards arrow straight a to the power of plus below space straight f left parenthesis straight x right parenthesis$
∴ f is not continuous at x = a, a ∈ I.
∴ function is discontinuous at every integral point.

277 Views