107. Discuss the continuity of the function defined by

Function f is defined for all real numbers except 0. Therefore domain of f is D₁ ∪ D₂ where
D₁ = {.x∈R : r < 0 }, D₂ = {x ∈  R : x > 0}
Now two cases arise :
Case 1: Let c ∈ D₁. In this case f(x) = x + 2.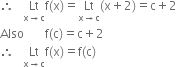

∴ f (x) is continuous at x = c
But c is any point of D₁.
∴ f is continuous in D₁.
Case II : Let c ∈ D₂. In this case f(x) = –x + 2.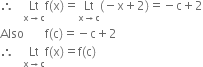

∴ f(x) is continuous at x = c.
But c is any point of D₂.
∴ f is continuous in D₂.
Now f is continuous at all points in the domain of f. f
∴ f is continuous.