108.
Discuss the continuity of the function f given by
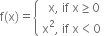
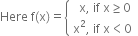
Function f is defined for all real numbers.
Now domain of f is divided into three disjoint subsets
D
1 = {.x ∈ R : x < 0}, D
2 = { 0}, D
3 = [x ∈ R : x > 0} of the real line.
Now three cases arise :
Case I : Let c ∈ D1 In this case f(x)=x
2
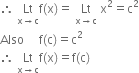
Case II : Let c ∈ D
3. In this case f(x)=x
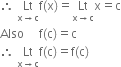
∴ f is continuous at x = c.
But c is any point of D
3.
∴ f is continuous in D
3.
Case III : We discuss continuity of f at x=0where f(x)=x
2
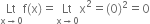
Now f is defined at x = 0
and f(0) = 0
∴ f is continuous at x = 0.
From three cases, it is clear that f is continuous at every point of domain and so f is continuous function.
72 Views
Short Answer Type
Long Answer Type
Switch
