Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Continuity and Differentiability

Short Answer Type

101. Find the value of k so that the function f is continuous at the indicated point

straight f left parenthesis straight x right parenthesis equals open curly brackets table attributes columnalign left end attributes row cell space straight k space straight x squared comma space straight x greater or equal than 1 end cell row cell space 4 space space space space comma space straight x less than 1 end cell end table close at space straight x equals 1

76 Views

102. Find the value of k so that the function f is continuous at the indicated point

straight f left parenthesis straight x right parenthesis equals open curly brackets table attributes columnalign left end attributes row cell straight k space straight x squared comma space straight x less or equal than 2 end cell row cell 3 space space space space comma space straight x greater than 2 end cell end table close at space straight x equals 2

77 Views

103. Find the value of k so that the function f is continuous at the indicated point

straight f left parenthesis straight x right parenthesis equals open curly brackets table attributes columnalign left end attributes row cell straight k space straight x plus 1 space space comma space straight x less or equal than 5 end cell row cell 3 x minus 5 space space space comma space straight x greater than 5 end cell end table close at space straight x equals 5

90 Views

104. Find the value of k so that the function f is continuous at the indicated point

straight f left parenthesis straight x right parenthesis equals open curly brackets table attributes columnalign left end attributes row cell straight k left parenthesis straight x squared minus 2 straight x space right parenthesis comma space if space straight x less than 0 end cell row cell space space cos space straight x space space space space space comma space if space straight x greater or equal than 0 end cell end table close at space straight x equals 0

73 Views

105. Discuss the continuity of the function f defined by

straight f left parenthesis straight x right parenthesis equals open curly brackets table attributes columnalign left end attributes row cell straight x plus 2 comma space if space straight x less or equal than 1 end cell row cell straight x minus 2 comma space if space straight x greater than 1 end cell end table close

83 Views

106. Find all the points of discontinuity of the function f defined by

straight f left parenthesis straight x right parenthesis equals open curly brackets table row cell straight x plus 2 comma space if space straight x less than 1 end cell row cell space space space space 0 comma space space space if space straight x equals 1 end cell row cell straight x minus 2 comma space if space straight x greater than 1 end cell end table close

90 Views

107. Discuss the continuity of the function defined by

straight f left parenthesis straight x right parenthesis equals open curly brackets table attributes columnalign left end attributes row cell straight x plus 2 comma space space space space space if space straight x less than 0 end cell row cell negative straight x plus 2 comma space if space straight x greater than 0 end cell end table close

87 Views

108. Discuss the continuity of the function f given by

straight f left parenthesis straight x right parenthesis equals open curly brackets table attributes columnalign left end attributes row cell space space straight x comma space if space straight x greater or equal than 0 end cell row cell straight x squared comma space if space straight x less than 0 end cell end table close

72 Views

109. Find all points of discontinuity of f, where f is defined by

straight f left parenthesis straight x right parenthesis equals open curly brackets table attributes columnalign left end attributes row cell 2 straight x plus 3 comma space if space straight x less or equal than 2 end cell row cell 2 straight x minus 3 comma space if space straight x greater than 2 end cell end table close

77 Views

Long Answer Type

110. Find all points of discontinuity of f, where f is defined by
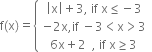
$straight f left parenthesis straight x right parenthesis equals open curly brackets table row cell open vertical bar straight x close vertical bar plus 3 comma space if space straight x less or equal than negative 3 end cell row cell negative 2 straight x comma if space minus 3 less than straight x greater than 3 end cell row cell 6 straight x plus 2 space space comma space if space straight x greater or equal than 3 end cell end table close$

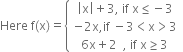
Here space straight f left parenthesis straight x right parenthesis equals open curly brackets table row cell open vertical bar straight x close vertical bar plus 3 comma space if space straight x less or equal than negative 3 end cell row cell negative 2 straight x comma if space minus 3 less than straight x greater than 3 end cell row cell 6 straight x plus 2 space space comma space if space straight x greater or equal than 3 end cell end table close

Function f is defined for all points of the real line.
Let c be any real number.
Five cases arise :
Case I: c < –3

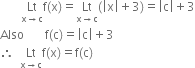
$space space space space space space space Lt with straight x rightwards arrow straight c below straight f left parenthesis straight x right parenthesis equals Lt with straight x rightwards arrow straight c below left parenthesis open vertical bar straight x close vertical bar plus 3 right parenthesis equals open vertical bar straight c close vertical bar plus 3 Also space space space space space space space straight f left parenthesis straight c right parenthesis equals open vertical bar straight c close vertical bar plus 3 therefore space space Lt with straight x rightwards arrow straight c below straight f left parenthesis straight x right parenthesis equals straight f left parenthesis straight c right parenthesis$
∴ f is continuous at all point x < – 3
Case II: c = –3

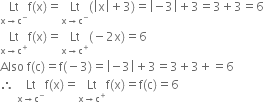
$Lt with straight x rightwards arrow straight c to the power of minus below straight f left parenthesis straight x right parenthesis equals Lt with straight x rightwards arrow straight c to the power of minus below left parenthesis open vertical bar straight x close vertical bar plus 3 right parenthesis equals open vertical bar negative 3 close vertical bar plus 3 equals 3 plus 3 equals 6 Lt with straight x rightwards arrow straight c to the power of plus below straight f left parenthesis straight x right parenthesis equals Lt with straight x rightwards arrow straight c to the power of plus below left parenthesis negative 2 straight x right parenthesis equals 6 Also space straight f left parenthesis straight c right parenthesis equals straight f left parenthesis negative 3 right parenthesis equals open vertical bar negative 3 close vertical bar plus 3 equals 3 plus 3 plus equals 6 therefore space Lt with straight x rightwards arrow straight c to the power of minus below straight f left parenthesis straight x right parenthesis equals Lt with straight x rightwards arrow straight c to the power of plus below straight f left parenthesis straight x right parenthesis equals straight f left parenthesis straight c right parenthesis equals 6$
∴ f is continuous at x = – 3
Case III: – 3 < c < 3
f(x) = – 2 x is a continuous function as it is a polynomial.
Case IV : c = 3

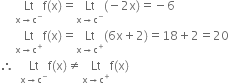
space space space space space Lt with straight x rightwards arrow straight c to the power of minus below straight f left parenthesis straight x right parenthesis equals Lt with straight x rightwards arrow straight c to the power of minus below left parenthesis negative 2 straight x right parenthesis equals negative 6 space space space space space Lt with straight x rightwards arrow straight c to the power of plus below straight f left parenthesis straight x right parenthesis equals Lt with straight x rightwards arrow straight c to the power of plus below left parenthesis 6 straight x plus 2 right parenthesis equals 18 plus 2 equals 20 therefore space space Lt with straight x rightwards arrow straight c to the power of minus below straight f left parenthesis straight x right parenthesis not equal to Lt with straight x rightwards arrow straight c to the power of plus below straight f left parenthesis straight x right parenthesis

∴ f is discontinuous at x = 3.
Case V ; c > 3

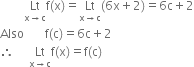
$space space space space space space space space Lt with straight x rightwards arrow straight c below straight f left parenthesis straight x right parenthesis equals Lt with straight x rightwards arrow straight c below left parenthesis 6 straight x plus 2 right parenthesis equals 6 straight c plus 2 Also space space space space space space space straight f left parenthesis straight c right parenthesis equals 6 straight c plus 2 therefore space space space space space Lt with straight x rightwards arrow straight c below straight f left parenthesis straight x right parenthesis equals straight f left parenthesis straight c right parenthesis$
∴ f is continuous at all points x > 3.

79 Views