 Multiple Choice Questions
Multiple Choice QuestionsIf f(x) is a function such that f'(x) = (x - 1)2(4 - x), then
f(0) = 0
f(x) is increasing in (0, 3)
x = 4 is a critical point of f(x)
f(x) is decreasing in (3, 5)
B.
f(x) is increasing in (0, 3)
C.
x = 4 is a critical point of f(x)
Given, f' (x) = (x- 1)2 (4 - x)
The sign scheme of f' (x)
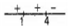
Clearly, f(x) is increasing, for
Since, f'(x) = 0 at x = 4
So, x = 4 is a critical point
And, f(x) is increasing in (0, 3)
Let f: [2, 2] R be a continuous function such that f(x) assumes only irrational values. If , then
f(0) = 0
Let [x] denotes the greatest integer less than or equal to x. Then, the value of · which the function
f(x) = is continuous at x = 0, is
For all real values of a0, a1, a2, a3 satisfying , the equation a0 + a1x + a2x + a3x3 = 0 has a real root in the interval
[0, 1]
[- 1, 0]
[1, 2]
[- 2, - 1]
f is discontinuous for all x
f is continuous for all x
f is discontinuous at x = k, where k is an integer
f is continuous at x = k, where k is an integer
