 Multiple Choice Questions
Multiple Choice QuestionsThe number of points, where f(x) = [sin(x) + cos(x)] (where [] denotes the greatest integerfunction) and x (0, 2) is not continuous, is
3
4
5
6
If 2a + 3b + 6c = 0, then the equation ax2 + bx + c = 0 has atleast one real root in
(0, 1)
None of the above
If f(x) = , then f(x) has
local minimum at x = 1
local maximum at x = 1
Both local maximum and local minimum at x = 1
None of the above
B.
local maximum at x = 1
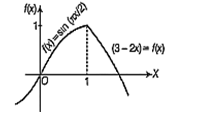
From the above graph of function, we see tha tf(x) has local maxima at x = 1.
Let f : R R be a differentiable function and f(1) = 4. Then, the value of is
8f'(1)
4f'(1)
2f'(1)
f'(1)
If f''(x) = - f(x) and g(x) = f'(x) anf F(x) = and given that F(5) = 5, then the value of F(10) is
15
0
5
10
A function g defined for all real x > 0 satisfies g(1) = 1, g'(x2) = x3 for all x > 0, then value of g(4) is
3
None of these
A particle moving on a curve has the position at a time t is given by x = f'(t)sin(t) + f'(t)cos(t), y = f'(t)cos(t) - f'(t)sin(t), where f is a twice differentiable function. Then, the velocity of the particle at time t is
f'(t) + f''(t)
f'(t) - f''(t)
f'(t) + f'''(t)
f'(t) - f''(t)
f(x) and g(x) are differentiable in the interval [0, 1] such that f(0) = 2, g(0) = 0, f(1) = 6, g(1) = 2, then Rolle's theorem is applicable for which of the following in [0, 1] ?
f(x) - g(x)
f(x) - 2g(x)
f(x) + 3g(x)
None of the above
The positive root of equation x2 - 2x - 5 = 0 lies in the interval
{0, 1}
(1, 2)
(2, 3)
(3, 4)
