Short Answer TypeFind the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, – 3) and B is (1, 4).
If A and B are (– 2, – 2) and (2, – 4), respectively, find the coordinates of P such that 
and P lies on the line segment Ab.
Long Answer TypeFind the coordinates of the points which divide the line segment joining A(– 2, 2) and B(2, 8) into four equal parts.
Find the area of a rhombus if its vertices are (3, 0), (4, 5), (– 1, 4) and (– 2, – 1) taken in order.
Short Answer TypeIn each of the following find the value of ‘k’, for which the points are collinear
(7, –2), (5, 1), (3, k)
In each of the following find the value of ‘k’, for which the points are collinear
(8, 1), (k, – 4), (2, –5)
Let the given points be A(8, 1), B(K, -4) and C(2, -5).
Here, we have
x1 = 8, y1 = 1
x2 = K, y2 = -4
and x3 = 2, y3 = -5
Now, Area of ∆ABC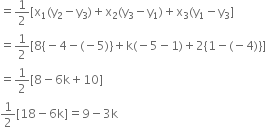
If the points are collinear, then area of the triangle = 0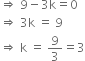
Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, –1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.
Long Answer TypeFind the area of the quadrilateral whose vertices, taken in order, are (– 4, – 2), (– 3, – 5), (3, – 2) and (2, 3).
Switch
