188.
The centre of a circle is (2α - 1, 7) and it passes through the point (- 3, - 1). If the diameter of the circle is 20 units, then find the value(s) of α.
Let co-ordinates of centre be 0(2α - 1,7), which passes through the point A(- 3, - 1).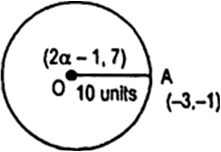
Fig. 7.23(A)
Now OA = 10 units
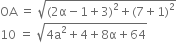
Squaring
100 = 4α2 + 8α + 68
4α2 + 8α - 32 = 0
α2 + 2α - 8 = 0
α2 + 4α + 2α - 8 = 0
α(α + 4) + 2(α - 8) = 0
(α - 4) (α - 2) = 0
α = -4, α = 2.
1083 Views
 Short Answer Type
Short Answer Type
![]()
