 Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type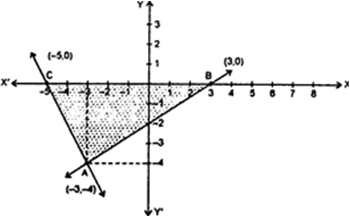

 Long Answer Type
Long Answer TypeFig. 7.28A.
Let the given points be A(3, -1) and B(-6, 5).
Let P and Q be the points of trisection of AB.
Then, AP = PQ = QB = 1
Thus ‘P’ divides AB in the ratio 1 : 2.
Here, we have x1 = 1, y1 = -2
x2 = -3, y2 = 4
and m1 = 1 m2 = 2
∴ The co-ordinates of ‘P’ are given by
Case II.![]()
Fig. 7.29.
Now ‘Q’ divides AB in the ratio 2 : 1.
Here, we have x1 = 1, y = -2
x2 = -3, y2 = 4
and m1 = 2 m2 = 1
∴ The co-ordinates of ‘Q’ are given by

Hence, the co-ordinates of the points of trisection are ![]()
