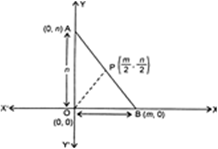
Short Answer Type
Short Answer Type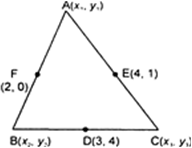
Fig. 7.33.
Let D(3, 4), E(4. 1), F(2, 0) are the mid-points of sides BC, CA and AB respectively. Since D is the mid-point of BC.![]()
Similarly, E and F are mid-points of CA and AB respectively.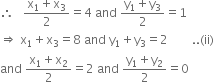
⇒ x1 + x2 = 4 and y1 + y2 = 0 ...(iii)
From (i), (ii) and (iii), we get
2 (x1 + x2 + x3) = 18 and 2(y1 + y2 + y3) = 10
⇒ x1 + x2 + 3, = 9 and y1 + y2 + y3 = 5 ...(iv)
From (i) and (iv), we get
x1 + 6 = 9 and y1 + 8 = 5
⇒ x1 = 3 and y1 = -3
∴Co-ordinates of A are (3, -3)
From (ii) and (iv), we get
x2 + 8 = 9 and y2 + 2 = 5
⇒ x2 = 1 and y2 = 3
∴ Co-ordinates of B are (1, 3)
From (ii) and (iv), we get
4 + x3 = 9 and 0 + y3 = 5
⇒ x3 = 5 and y3 = 5
∴ Coordinates of C are (5, 5)
Hence, the vertices of ∆ABC are A(3, -3), B(1, 3), C(5, 5).