225. The mid-points of the sides of a triangle are (3, 4), (4, 6) and (5, 7). Find the coordinates of the vertices of the triangle.

). If P(3, 4), Q(4, 6) and R(5, 7) are the midpoints of AB, BC and CA. Then,

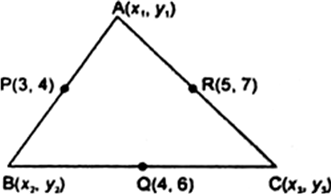
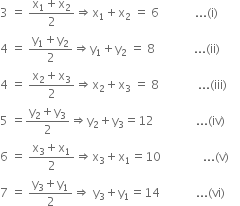
Adding (i), (iii) and (v), we get

2(x₁ + x₂ + x₃) = 6 + 8 + 10 = 24

⇒    x₁ + x₂ + x₃ = 12    ...(vii)

From (i) and (vii), we get x₃ = 12 - 6 = 6
From (iii) and (vii), we get v₁ = 12 - 8 = 4
From (v) and (vii), we get x₂ = 12 - 10 = 2
Now, adding (ii), (iv) and (vi), we get
20(y₁ + y₂ + y₃) = 8 + 12 + 14 = 34
⇒    y₁ + y₂ + y₃ = 17    (viii)
From (ii) and (viii), we get y₃ = 17 - 8 = 9
From (iv) and (viii), we get y₁ = 17 - 12 = 5
From (vi) and (viii), we get y₂ 17 - 14 = 3
Hence, the vertices of ∆ABC are A(4, 5), B(2, 3), C(6, 9)