 Short Answer Type
Short Answer Type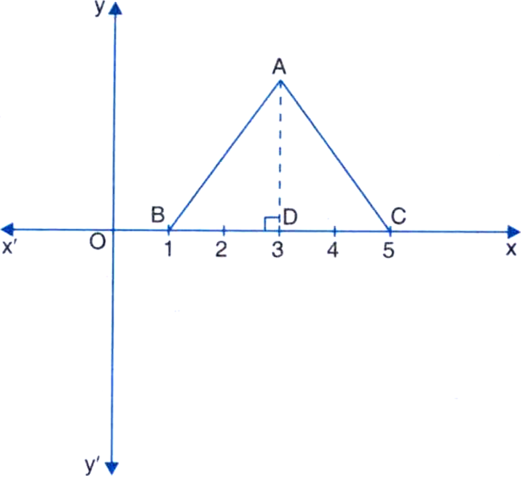

‚ąĶ ‚ąÜPQR is an equilateral triangle
‚ąī PQ = PR = QR
‚áí PQ = QR
‚áí PQ = 4
OQ = 2
In right triangle POQ,
OP2 + OQ2 = PQ2 |By Pythagoras Theorem
⇒ OP2 + (2)2 = (4)2![]()
Find the co-ordinates of a point:
(i)    whose ordinate is 6 and lies on y-axis.
(ii)    whose abscissa is -3 and lies on x-axis.
In which quadrant, can a point have:
(i)      abscissa equal to its ordinate
(ii)     ordinate equal in magnitude to abscissa
(iii)    ordinate equal and opposite of abscissa
(iv)    abscissa twice that of the ordinate.

(i)    The abscissa and the ordinate of the point B are _ _ _ and _ _ _, respectively. Hence the coordinates of B are (_ _, _ _).
(ii)    The x-coordinate and the y-coordinate of the point M are _ _ _ and _ _ _, respectively. Hence the coordinates of M are (_ _ _, _ _ _).
(iii)    The x-coordinate and the y-coordinate of the point L are _ _ _ and _ _ _, respectively. Hence the coordinates of L are (_ _, _ _).
(iv)    The x-coordinate and the y-coordinate of the point S are _ _ _ and _ _ _, respectively. Hence the coordinates of S are (_ _, _ _).
In which quadrant do the given points lie?
(a) (2, -1)    (b) (-1, 7)
(c) (-2, -3)    (d) (4, 5)
