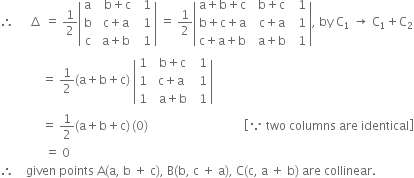If a, b, c are in A.P, then the determinant

• 0

• 1

• v

• v

Find the area of the triangle, whose vertices are (3, 1), (4, 3) and (-5, 4).

Find the area of the triangle with vertices at the points given in each of the following:
(1, 0)  (6,0), (4, 3) 

Find the area of the triangle with vertices at the points given in each of the following:
(2, 7), (1, 1), (10, 8)

Find the area of the triangle with vertices at the points given in each of the following:
(–2,–3), (3, 2), (–1,–8)

137.

Show that points A(a, b +  c),  B(b, c + a),  C(c, a + b) are collinear.

Using determinants, show that the points (11, 7), (5, 5) and (– 1, 3) are collinear.

Determine x so that the points (3, 2), (x, 2) and (8, 8) lie on a line.