Trying to find the right answer to this..

Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Write the minors and cofactors of the elements of following determinants:
$open vertical bar table row 1 cell space space space 0 end cell 4 row 3 cell space space 5 end cell cell negative 1 end cell row 0 cell space 1 end cell cell space 2 end cell end table close vertical bar$

79 Views

Long Answer Type

152. Find the minors and cofactors of the elements of the determinant:

open vertical bar table row 2 cell space space space minus 3 end cell cell space space space 5 end cell row 6 cell space space 0 end cell cell space space space 4 end cell row 1 cell space space 5 end cell cell negative 7 end cell end table close vertical bar

and verify that a₁₁A₃₁ + a₁₃A₃₃ = 0.

102 Views

Short Answer Type

153. Write the minors and cofactors of the elements of following determinants:

open vertical bar table row 1 cell space space 0 end cell cell space space 0 end cell row 0 cell space space 1 end cell cell space space 0 end cell row 0 cell space 0 end cell cell space space 1 end cell end table close vertical bar

74 Views

154.

Using cofactors of elements of second row, evaluate:
$increment space equals space open vertical bar table row 5 cell space space 3 end cell cell space space 8 end cell row 2 cell space space 0 end cell cell space space 1 end cell row 1 cell space 2 end cell cell space space 3 end cell end table close vertical bar$

98 Views

155.

Using cofactors of elements of third column, evaluate:
$increment space equals space open vertical bar table row 1 cell space space straight x end cell cell space space yz end cell row 1 cell space space straight y end cell cell space space zx end cell row 1 cell space space straight z end cell cell space space xy end cell end table close vertical bar.$

74 Views

Multiple Choice Questions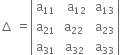

156. If

increment space equals open vertical bar table row cell straight a subscript 11 end cell cell space space straight a subscript 12 end cell cell space straight a subscript 13 end cell row cell straight a subscript 21 end cell cell straight a subscript 22 end cell cell space straight a subscript 23 end cell row cell straight a subscript 31 end cell cell space straight a subscript 32 end cell cell space straight a subscript 33 end cell end table close vertical bar

and A_ij is Cofactors of a_ij, then value of ∆ is given by

a₁₁A₃₁ + a₁₂A₃₂ + a₁₃A₃₃
a₁₁A₁₁ + a₁₂A₂₁ + a₁₃A₃₁
a₂₁A₁₁ + a₂₂A₁₂ + a₂₃A₁₃
a₂₁A₁₁ + a₂₂A₁₂ + a₂₃A₁₃

80 Views

Short Answer Type

157.
If A, B, C are square matrices of the same order such that AB = BA = I and AC = CA = I then B = C.

We have
AB = BA = I    ...(1)
and AC = CA = I    ...(2)
Now B = BI
= B(AC)    [∵ of (2)]
= (BA) C    [∵ of associative properties of multiplication]
= IC    [∵ of (1)]
= C
∴ B = C
Hence the result.
Note : AB = BA = I ⇒ B is inverse of A
Again AC = CA = 1 ⇒ C is inverse of A
Also B = C
∴ inverse of a matrix A, if it exists, is unique.

80 Views

158.

Find adj A for $straight A space equals space open square brackets table row 2 cell space space space 3 end cell row 1 cell space space space 4 end cell end table close square brackets.$

69 Views

159.

Find the adjoint of the matrix $open square brackets table row 1 cell space space space space space 2 end cell row 3 cell space space space space 4 end cell end table close square brackets.$