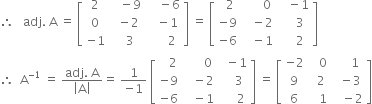Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

If $straight A space equals open square brackets table row 2 cell space space space space space space space 3 end cell row 1 cell space space minus 4 end cell end table close square brackets comma space straight B space equals space open square brackets table row cell space space space 1 end cell cell space space space space minus 2 end cell row cell negative 1 end cell cell space space space space space space 3 end cell end table close square brackets comma$
verify that (AB)^–1 = B^–1 A^–1

83 Views

192.

Let $straight A space equals space open square brackets table row 3 cell space space space 7 end cell row 2 cell space space 5 end cell end table close square brackets space and space straight B space equals space open square brackets table row 6 cell space space 8 end cell row 7 cell space space 9 end cell end table close square brackets comma$ verify that (AB)^–1 = B^–1 A^–1.

89 Views

193. Verify that (AB)^–1 = B^–1 A^–1 for the matrices A and B where

straight A space equals space open square brackets table row 3 cell space space 2 end cell row 7 cell space space 5 end cell end table close square brackets comma space space straight B space equals space open square brackets table row 4 cell space space 6 end cell row 3 cell space space 2 end cell end table close square brackets

74 Views

194. Verify that (AB)^–1 = B^–1 A^–1 for the matrices A and B where

straight A space equals open square brackets table row 3 cell space space 2 end cell row 7 cell space space 5 end cell end table close square brackets comma space space straight B space equals space open square brackets table row 6 cell space space space space 7 end cell row 8 cell space space space space 9 end cell end table close square brackets

71 Views

195. Verify that (AB)^–1 = B^–1 A^–1 for the matrices A and B where

straight A space equals space open square brackets table row 2 cell space space space 1 end cell row 5 cell space space space 3 end cell end table close square brackets comma space space space straight B space equals space open square brackets table row 4 cell space space space 5 end cell row 3 cell space space 4 end cell end table close square brackets

73 Views

Short Answer Type

196.

Find (AB)^–1 if $straight A space equals space open square brackets table row 3 cell space 4 end cell row 1 cell space 1 end cell end table close square brackets comma space space straight B to the power of negative 1 end exponent space equals space open square brackets table row 4 cell space space 3 end cell row 2 cell space space 1 end cell end table close square brackets$

73 Views

197.

Find (AB)^–1 if $straight A space equals space open square brackets table row 5 cell space space 0 end cell row 2 cell space space space 3 end cell end table close square brackets comma space space space straight B to the power of negative 1 end exponent space equals space open square brackets table row 1 cell space space space 2 end cell row 1 cell space space 4 end cell end table close square brackets$

87 Views

Long Answer Type

198.

Find the inverse of the matrix
$straight A space equals space open square brackets table row cell negative 1 end cell cell space space 1 end cell cell space space 2 end cell row cell space space space 3 end cell cell negative 1 end cell cell space space 1 space end cell row cell space minus 1 end cell cell space space 3 end cell cell space 4 end cell end table close square brackets.$

72 Views

199. Find the inverse of the matrix:
$open square brackets table row 1 cell space space space minus 1 end cell cell space space space space space space 2 end cell row 0 cell space space space space space space 2 end cell cell space space space minus 3 end cell row 3 cell space space space minus 2 end cell cell space space space space space space 4 end cell end table close square brackets.$

Let $straight A space equals space open square brackets table row 1 cell space space minus 1 end cell cell space space space space space space 2 end cell row 0 cell space space space space space 2 end cell cell space space minus 3 end cell row 3 cell space space minus 2 end cell cell space space space space 4 end cell end table close square brackets$

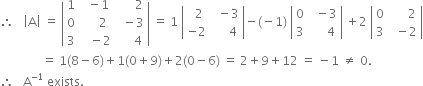
$therefore space space space open vertical bar straight A close vertical bar space equals space open vertical bar table row 1 cell space space minus 1 end cell cell space space space space space space 2 end cell row 0 cell space space space space space 2 end cell cell space space minus 3 end cell row 3 cell space space space minus 2 end cell cell space space space space space 4 end cell end table close vertical bar space equals space 1 space open vertical bar table row cell space space 2 end cell cell space space minus 3 end cell row cell negative 2 end cell cell space space space space space 4 end cell end table close vertical bar minus left parenthesis negative 1 right parenthesis space open vertical bar table row 0 cell space space minus 3 end cell row 3 cell space space space space space 4 end cell end table close vertical bar space plus 2 space open vertical bar table row 0 cell space space space space space space 2 end cell row 3 cell space space minus 2 end cell end table close vertical bar space space space space space space space space space space space space space space equals space 1 left parenthesis 8 minus 6 right parenthesis plus 1 left parenthesis 0 plus 9 right parenthesis plus 2 left parenthesis 0 minus 6 right parenthesis space equals space 2 plus 9 plus 12 space equals space minus 1 space not equal to space 0. therefore space space space straight A to the power of negative 1 end exponent space exists.$

Co-factors of the elements of first row of | A | are
$open vertical bar table row cell space space 2 end cell cell space space space minus 3 end cell row cell negative 2 end cell cell space space space space space space 4 end cell end table close vertical bar comma space space space space space minus open vertical bar table row 0 cell space space space minus 3 end cell row 3 cell space space space space space space 4 end cell end table close vertical bar comma space space open vertical bar table row 0 cell space space space space space space space 2 end cell row 3 cell space space space minus 2 end cell end table close vertical bar$
i.e. 2, –9, — 6 respectively.
Co-factors of the elements of second row of | A | are
$negative open vertical bar table row cell negative 1 end cell cell space space space 2 end cell row cell negative 2 end cell cell space space 4 end cell end table close vertical bar comma space space space open vertical bar table row 1 cell space space space space space space space 2 end cell row 3 cell space space space space space space space 4 end cell end table close vertical bar comma space space space space minus open vertical bar table row 1 cell space space space space minus 1 end cell row 3 cell space space space space space minus space 2 end cell end table close vertical bar$
i.e. 0, – 2, – 1 respectively.
Co-factors of the elements of third row of | A | are
$open vertical bar table row cell negative 1 end cell cell space space space space space space space space 2 end cell row cell space 2 end cell cell space space space minus 3 end cell end table close vertical bar comma space space space space space minus open vertical bar table row 1 cell space space space space space space space 2 end cell row 0 cell space space space minus 3 end cell end table close vertical bar comma space space space space space open vertical bar table row 1 cell space space space minus 1 end cell row 0 cell space space space space space 2 end cell end table close vertical bar$
i.e. – 1, 3, 2 respectively.
$therefore space space space adj. space straight A space equals space open square brackets table row 2 cell space space space minus 9 end cell cell space space space space minus 6 end cell row 0 cell space space minus 2 end cell cell space space space minus 1 end cell row cell negative 1 end cell cell space space space 3 end cell cell space space space space space space 2 end cell end table close square brackets space equals space open square brackets table row cell space space 2 end cell cell space space space space space space 0 end cell cell space space space minus 1 end cell row cell negative 9 end cell cell space space space minus 2 end cell cell space space space space 3 end cell row cell negative 6 end cell cell space space space minus 1 end cell cell space space space space 2 end cell end table close square brackets therefore space space straight A to the power of negative 1 end exponent space equals space fraction numerator adj. space straight A over denominator open vertical bar straight A close vertical bar end fraction equals space fraction numerator 1 over denominator negative 1 end fraction space open square brackets table row cell space space space 2 end cell cell space space space space space space 0 end cell cell space space minus 1 end cell row cell negative 9 end cell cell space space space minus 2 end cell cell space space space space 3 end cell row cell negative 6 end cell cell space space space minus 1 end cell cell space space space space space 2 end cell end table close square brackets space equals space open square brackets table row cell negative 2 end cell cell space space space 0 end cell cell space space space space space 1 end cell row 9 cell space space 2 end cell cell space space minus 3 end cell row 6 cell space space space 1 end cell cell space space space minus 2 end cell end table close square brackets$

74 Views

200.

If $straight A space equals space open square brackets table row 0 cell space space space 0 end cell cell space space 1 end cell row 0 cell space space 1 end cell cell space space 0 end cell row 1 cell space space 0 end cell cell space space 0 end cell end table close square brackets comma$ show that A^–1 = A.

72 Views