 Long Answer Type
Long Answer TypeCompute (AB)1 where:![]()
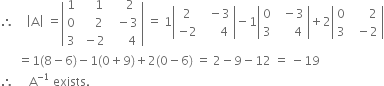
i.e.. — 8, – 2, 5 respectively
Co-factors of the elements of third row of | A | are![]()
i.e., -7, 3, 2 respectively.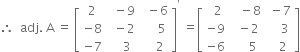
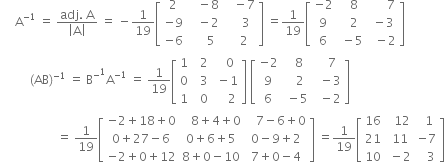
 Multiple Choice Questions
Multiple Choice Questions Short Answer Type
Short Answer TypeExamine the consistency of the system of equations:
x+y+z = 1
2x + 3y + 2z = 2
ax+ay+2az = 4
