 Long Answer Type
Long Answer Type Multiple Choice Questions
Multiple Choice QuestionsIf A is an invertible matrix of order 2, then det (A–1) is equal to
det (A)
1
1
B.
We know that
![]()
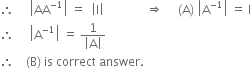
 Short Answer Type
Short Answer TypeExamine the consistency of the system of equations:
x+y+z = 1
2x + 3y + 2z = 2
ax+ay+2az = 4
