 Long Answer Type
Long Answer TypeExamine the consistency of the system of equations:
3x – y – 2z = 2
2y – z = – 1
3x – 5y = 3
The given equations are
3x – y – 2z = 2
0x + 2y – z = – 1
3x – 5y+Oz = 3
These equations can be written as![]()
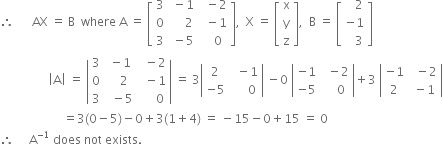
Cofactors of the elements of first row of | A | are![]()
i.e. 0 – 5, – (0 + 3), 0 – 6 i.e. – 5, – 3, – 6 respectively.
Cofactors of the elements of second row of | A | are![]()
i.e. – (0 – 10), 0 + 6, –(– 15 + 3) i.e. 10, 6, 12 respectively.
Co-factors of the elements of third row of | A | are![]()
i.e. 1 + 4, – (– 3 – 0), 6 – 0 i.e. 5, 3, 6 respectively.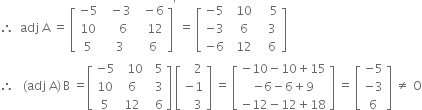
∴ solution does not exist and so system of equations is inconsistent.
 Short Answer Type
Short Answer TypeExamine the consistency of the system of equations:
5x – y + 4z = 5
2x + 3y + 5z = 2
5x – 2y + 6z = – 1
 Long Answer Type
Long Answer TypeExamine the consistencies of the system of equations:
3x – y + 2z = 3
2x + y + 3z =5
x - 2y - z = 1
Examine the consistencies of the system of equations:
x - y+ z = 3
2x - y – z = 2
– x – 2y + 2z = 1
 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type