 Long Answer Type
Long Answer TypeUsing matrices, solve the following system of equations:
2x + y ‚Äď 3r = 13
x + y ‚Äď z = 6
2x ‚Äď y + 4z = ‚Äď 12
The given equations are
2x + y ‚Äď 3 z = 13
x + y ‚Äď z ‚Äď 6
2x ‚Äď y + 4 z = ‚Äď 12
These equations can be written as
                     ![]()        
       
     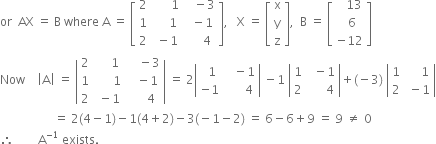
Co-factors of the elements of first row of | A | are![]()
i.e. 3, ‚Äď 6, ‚Äď 3 respectively.
Co-factors of the elements of second row of | A | are![]()
i.e. ‚Äď 1, ¬†14, ¬†4 respectively.
Co-factors of the elements of third row of | A | are![]()
i.e. ¬† 2, ‚Äď 1, 1 respectively.
Using matrices, solve the following system of linear equations.
3x + 4y + 2z = 8
2y ‚Äď3z = 3
x ‚Äď 2y + 6z = ‚Äď2 ¬†
Using matrices, solve the following system of linear equations:
x ‚Äď y = 3
2x + 3y + 4z = 17
y + 2 z = 7
Solve the following system of equations by matrix method:
3x ‚Äď 2y + 3z = 8
2x + y ‚Äď z = 1
4x ‚Äď 3y + 2z = 4
Solve the following system of equations by matrix method:
x ‚Äď y + z = 2
2x ‚Äď y = 0
2y ‚Äď z = 1¬†
Solve the following system of equations by matrix method:
2x ‚Äď y + z = ‚Äď 3
3 x ‚Äď z = ‚Äď 8
2x + 6y    = 2
