Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Solve by matrix method:
$3 over straight x plus 4 over straight y plus 7 over straight z space equals space 14 2 over straight x minus 1 over straight y plus 3 over straight z space equals space 4 1 over straight x plus 2 over straight y minus 3 over straight z space equals space 0$

92 Views

302.

Solve the system of the following equations:
$2 over straight x plus 3 over straight y plus 10 over straight z space equals space 4 4 over straight x minus 6 over straight y plus 5 over straight z space equals space 1 6 over straight x plus 9 over straight y minus 20 over straight z space equals space 2$

75 Views

303.

If $straight A space equals space open square brackets table row 2 cell space space space minus 3 end cell cell space space space space 5 end cell row 3 cell space space space space space 2 end cell cell space minus 4 end cell row 1 cell space space space 1 end cell cell space minus 2 end cell end table close square brackets comma$ find A^-^1,Using A^-¹, solve the following system of linear equations.
2x – 3y + 5z = 16
3x + 2y – 4z = – 4
x + y – 2z = – 3

75 Views

304.

If $straight A space equals space open square brackets table row 2 cell space space space minus 3 end cell cell space space space space 5 end cell row 3 cell space space space space 2 end cell cell negative 4 end cell row 1 cell space space space 1 end cell cell negative 2 end cell end table close square brackets comma$ find A ^–1 .
Using A^–1, solve the following system of linear equations.
2x – 3y + 5z = 11
3x + 2y – 4z = – 5
x + y – 2z = – 3

74 Views

305.

Compute A^–1 for the following matrix
$straight A space equals space open square brackets table row cell negative 1 end cell cell space space space space space 2 end cell cell space space space space 5 end cell row cell space space 2 end cell cell space space minus 3 end cell cell space space space 1 end cell row cell negative 1 end cell cell space space 1 end cell cell space space space space 1 end cell end table close square brackets.$
Hence solve the system of equations.
– x + 2y+ 5 z = 2
2x – 3y + Z = 15
– x + y + z = – 3

78 Views

306.

Compute A^–1 for the following matrix
$straight A space equals space open square brackets table row 1 cell space space space space space 2 end cell cell space space space 5 end cell row 1 cell space minus 1 end cell cell space minus 1 end cell row 2 cell space space space 3 end cell cell space minus 2 end cell end table close square brackets.$
Hence, solve the system of equations:
x + 2y + 5z = 10
x – y – z = – 2
2x + 3y – 2z = – 1

97 Views

307.

If $straight A equals space open square brackets table row 3 cell space space space minus 2 end cell cell space space space space space 1 end cell row 2 cell space space space space 1 end cell cell space minus 3 end cell row cell negative 1 end cell cell space space space 2 end cell cell space space space 1 end cell end table close square brackets comma$ Find A^–1.

Using A solve the following systems of linear equations:
3x – 2y + z = 2
2y + y – 3z = – 5
– x + 2y + z = 6.

75 Views

Short Answer Type

308.
Investigate for what values of a and b the simultaneous equations:
x + y + z = 6
x + 2y + 3z = 10
x + 2y + az = b have a unique solution.

The given equations are
x + y + z = 6
x + 2y + 3z = 10
x + 2y + az = b
These equations can be written as
$open square brackets table row 1 cell space space space 1 end cell cell space space space 1 end cell row 1 cell space space space 2 end cell cell space space space 3 end cell row 1 cell space space space 2 end cell cell space space space straight a end cell end table close square brackets space space space open square brackets table row straight x row straight y row straight z end table close square brackets space equals space open square brackets table row 16 row 10 row straight b end table close square brackets$

or $AX space equals space straight B space space where space straight A space equals space open square brackets table row 1 cell space space space 1 end cell cell space space 1 end cell row 1 cell space space 2 end cell cell space space 3 end cell row 1 cell space 2 end cell cell space space straight a end cell end table close square brackets space space open square brackets table row straight x row straight y row straight z end table close square brackets space space equals space open square brackets table row 6 row 10 row straight b end table close square brackets$
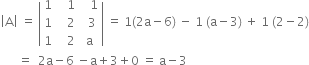
$open vertical bar straight A close vertical bar space equals space open vertical bar table row 1 cell space space space 1 end cell cell space space space 1 end cell row 1 cell space space space 2 end cell cell space space 3 end cell row 1 cell space space space 2 end cell cell space straight a space end cell end table close vertical bar space equals space 1 left parenthesis 2 straight a minus 6 right parenthesis space minus space 1 space left parenthesis straight a minus 3 right parenthesis space plus space 1 space left parenthesis 2 minus 2 right parenthesis space space space space space space equals space space 2 straight a minus 6 space minus straight a plus 3 plus 0 space equals space straight a minus 3$
Given system of equation has a unique solution
when | A | ≠ 0 i.e., a – 3 ≠ i.e., a ≠ 3, and b and may have any value.

86 Views

Long Answer Type

309.

The sum of three numbers is 6. If we multiply third number by 3 and add second number to it, we get 11. By adding first and third numbers, we get double of the second number. Represent it algebraically and find the numbers using matrix method.

86 Views

310. The cost of 4 kg. onion, 3 kg. wheat and 2 kg. rice is Rs. 60. The cost of 2 kg. onion, 4 kg. wheat and 6 kg. rice is Rs. 90. The cost of 6 kg. onion. 2 kg. wheat and 3 kg. rice is Rs. 70. Find cost of each item per kg. by matrix method.

77 Views