 Short Answer Type
Short Answer TypeIn the following, verify that the given functions, (explicit or implicit) is a solution of the corresponding differential equation:
![]()
Here, ![]()
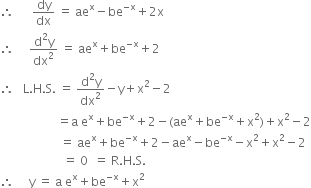
is a solution of the given differential equation.
