Long Answer TypeObserve the following tables and find if x and y are directly proportional.
(i)
|
X |
20 |
17 |
14 |
11 |
8 |
5 |
2 |
|
y |
40 |
34 |
28 |
22 |
16 |
10 |
4 |
(ii)
|
X |
6 |
10 |
14 |
18 |
22 |
26 |
30 |
|
y |
4 |
8 |
12 |
16 |
20 |
24 |
28 |
(iii)
|
X |
5 |
8 |
12 |
15 |
18 |
20 |
|
y |
15 |
24 |
36 |
60 |
72 |
100 |
Short Answer TypeIf we fix time period and the rate of interest, simple interest changes proportionally with principal. Would there be a similar relationship for compound interest? Why?
Long Answer TypeA mixture of paint is prepared by mixing 1 part of red pigments with 8 parts of base. In the following table, find the parts of base that need to be added.
Short Answer TypeIn question 2 above, if 1 part of a red pigment requires 75 mL of base, how much red pigment should we mix with 1800 mL of base?
A machine in a soft drink factory fills 840 bottles in six hours. How many bottles will it fill in five hours?
|
Number of bottles filled |
Number of hours |
|
840 |
6 |
|
X |
5 |
A photograph of a bacteria enlarged 50,000 times attains a length of 5 cm as shown in the diagram. What is the actual length of the bacteria? If the photograph is enlarged 20,000 times only, what would be its enlarged length?
In a model of a ship, the mast is 9 cm high, while the mast of the actual ship is 12 m high. If the length of the ship is 28m, how long is the model ship?
Long Answer TypeSuppose 2 kg of sugar contains 9 x 106 crystals. How many sugar crystals are there in (i) 5 kg of sugar? and (ii) 1.2 kg of sugar?
Solution: Let the required number of sugar crystals be x in 5 kg of sugar.
We have:
(i)
|
Weight of sugar |
Number of sugar crystals |
|
2 |
9 x 106 |
|
5 |
X |
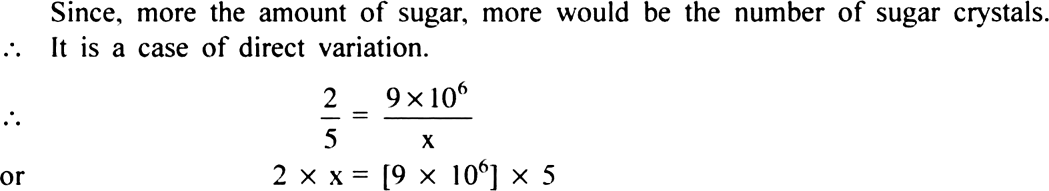
(ii) Let the number sugar crystals in 1.2 kg of sugar be y.
∴We have:
|
Weight of sugar |
Number of sugar crystals |
|
2 |
9 x 106 |
|
1.2 |
y |
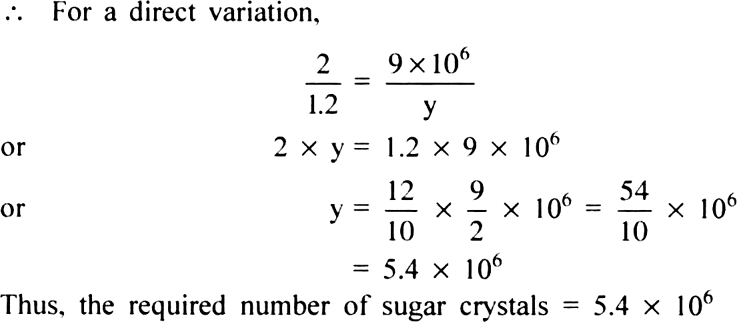
Short Answer TypeRashmi has a road map with a scale of 1 cm representing 18 km. She drives on a road for 72 km. What would be her distance covered in the map?
Switch
