 Long Answer Type
Long Answer TypeEvaluate the following integrals as the limit of a sum![]()
Comparing ![]() with
with ![]() ,
,
![]()
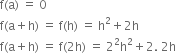
........ ............. .......... ........... ........
![]()
Now ![]()
![]()
![]()
![]() ]
]
![]()
![]()
![]()
![]()
![]()
![]()
 Short Answer Type
Short Answer Type