 Short Answer Type
Short Answer TypeFind the ratio in which the YZ-plane divides the line segment formed by joining the points (–2, 4, 7) and (3, –5, 8).
Find the ratio in which theВ join of P (2, 1, -1) and Q (3, 2, 4) is divided by XY-plane.
 Long Answer Type
Long Answer Type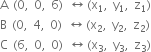
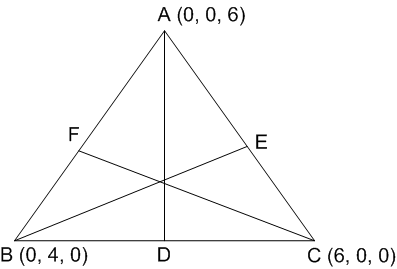
 Short Answer Type
Short Answer Type