191.

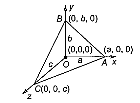
A plane meets the coordinate axes at A, B, C so that the centroid of the triangle ABC is (1, 2, 4). Then, the equation of the plane is

• x + 2y +4z =12

• 4x + 2y + z = 12

• x + 2y + 4z = 3

• 4x + 2y + z = 3

If (2, 3, - 3) is one end of a diameter of the sphere x² + y² + z² - 6x - 12y - 2z + 20 = 0, then the other end of the diameter is

• (4, 9, - 1)

• (4, 9, 5)

• (- 8, - 15, 1)

• (8, 15, 5)

The locus of a point such that the sum of its distances from the points (0, 2) and (0, - 2) is 6, is

• 9x² - 5y² = 45

• 5x² + 9y² = 45

• 9x² + 5y² = 45

• 5x² - 9y² = 45

The ratio in which the line joining (2, - 4, 3) and ( - 4, 5, - 6) is divided by the plane 3x + 2y + z - 4 = 0 is

• 2 : 1

• 4 : 3

• - 1 : 4

• 2 : 3

A plane passes through (2, 3, - 1) and is perpendicular to the line having direction ratios 3, - 4, 7. The perpendicular distance from the origin to this plane is

• $\frac{3}{\sqrt{74}}$

• $\frac{5}{\sqrt{74}}$

• $\frac{6}{\sqrt{74}}$

• $\frac{13}{\sqrt{74}}$

If the angles made by a straight line with thecoordinate axes are, $\mathrm{\alpha }, \frac{\mathrm{\pi }}{2} - \mathrm{\alpha }, \mathrm{\beta }, \mathrm{then} \mathrm{\beta } \mathrm{is} \mathrm{equal} \mathrm{to}$

• 0

• $\frac{\mathrm{\pi }}{6}$

• $\frac{\mathrm{\pi }}{2}$

• $\mathrm{\pi }$

The radius of the circle given by

x² + y² + z² + 2x - 2y - 2z - 19 = 0

• 4

• 3

• 2

• 1

If x-coordinate of a point P on the line joining the points Q(2, 2, 1) and R(5, 1, - 2) is 4, then the z-coordinate of P is

• - 2

• - 1

• 1

• 2

The equation of the sphere through the points (1, 0, 0), (0, 1, 0) and (1, 1, 1)and having the smallest radius

• $3\left({\mathrm{x}}^2 + {\mathrm{y}}^2 + {\mathrm{z}}^2\right) - 4\mathrm{x} - 4\mathrm{y} - 2\mathrm{z} + 1 = 0$

• $2\left({\mathrm{x}}^2 + {\mathrm{y}}^2 + {\mathrm{z}}^2\right) - 3\mathrm{x} - 3\mathrm{y} - \mathrm{z} + 1 = 0$

• $\left({\mathrm{x}}^2 + {\mathrm{y}}^2 + {\mathrm{z}}^2\right) - \mathrm{x} - \mathrm{y} - \mathrm{z} + 1 = 0$

• ${\mathrm{x}}^2 + {\mathrm{y}}^2 + {\mathrm{z}}^2 - 2\mathrm{x} - 2\mathrm{y} + 4\mathrm{z} + 1 = 0$

The origin is translated to (1, 2). The point(7, 5) in the old system undergoes the following transformations successively.

I. Moves to the new point under the given translation of origin.

II. Translated through 2 units along the negative direction of the new X-axis.

III. Rotated through an angle - about the 4 origin of new system in the clockwise direction. The final position of the point (7, 5) is

• $\left(\frac{9}{\sqrt{2}}, \frac{- 1}{\sqrt{2}}\right)$

• $\left(\frac{7}{\sqrt{2}}, \frac{1}{\sqrt{2}}\right)$

• $\left(\frac{7}{\sqrt{2}}, \frac{- 1}{\sqrt{2}}\right)$

• $\left(\frac{5}{\sqrt{2}}, \frac{- 1}{\sqrt{2}}\right)$