Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Linear Equations in Two Variables

Short Answer Type

31. 5. If x = –2, y = 6 is solution of equation 3ax + 2by = 6, then find the value of b from 2(a – 1) + 2(3b – 4) = 4.

If x = –2, y = 6 is solution of equation
3ax + 2by = 6, then

3a(-2) + 2b(6) = 6
$rightwards double arrow$ -6a + 12b = 6
$rightwards double arrow$ -a + 2b = 1 ...(1)
| dividing throughout by 6

Also

2(a - 1) + 2(3b - 4) = 4
$rightwards double arrow$ 2a - 2 + 6b -8 = 4
$rightwards double arrow$ 2a + 6b = 14
$rightwards double arrow$ a + 3b = 7 ....(2)
| Dividing throughout by 2
Adding (1) and (2), we get

5b = 8 $rightwards double arrow$ b = $8 over 5$
Putting b = $8 over 5$ in (1), we get

$negative straight a plus 2 open parentheses 8 over 5 close parentheses equals 1$
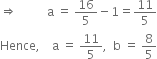
$rightwards double arrow space space space space space space space space space space straight a space equals space 16 over 5 minus 1 equals 11 over 5 Hence comma space space space space straight a space equals space 11 over 5 comma space space straight b space equals space 8 over 5$

181 Views

32. The coordinates of the points given in the following table represent some of the solutions of the equation

y equals 3 over 2 space space x space minus 1

Find the missing values. Also find the coordinates of the points where the line cuts x-axis and y-axis.

118 Views

33. Find the coordinates of the points where the line representing the equation

straight x over 4 equals 1 minus y over 6

cuts the x-axis and the y-axis.

115 Views

34. Determine the point on the graph of the equation 2x + 5y = 20 where x-coordinate is

5 over 2

times its ordinate.

228 Views

35.

Find four different solutions of the equation

x + 2y = 6.

399 Views

36.

Find two solutions for each of the following equations:

(i) 2x – 3y = 12 (ii) 2x – 5y = 0

(iii) 3y – 4 = 0.

206 Views

37.

Find the value of a so that the following equation may have x = 1, y = 1 as a solution:

3x + ay = 6

105 Views

38.

Write the equation $straight y square root of 3 equals 8 straight x plus square root of 5$ in the form of ax + by + c =0. Check whether (0, 1) and $left parenthesis square root of 3 comma space 9 right parenthesis$ are the solutions of the equation.

100 Views

39. Find three different solutions for the equation 3x – 4y = –12.

270 Views

40. Find three different solutions for the equation 6x – 8y + 32 = 0.

187 Views