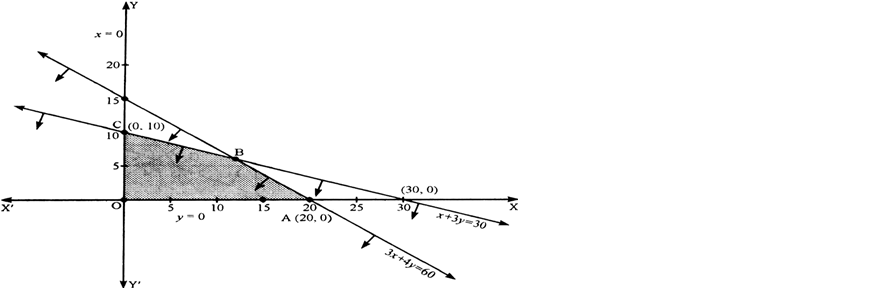
Clearly, x ≥ 0, y ≥ 0 means that the solution set lies in the first quadrant.
Now, we draw the graph of line 3x + 4y = 60

x             0            20
y             15           0

Now, we consider the point O(0, 0) i.e., origin.
Substitute in inequality 3x + 4y ≤ 60, i.e., 3(0) + 4(0) ≤ 60 or 0 ≤ 60 which is true.
Therefore, we mark that region which contains origin.
Now, we draw the graph of line x + 3y = 30

x               0          30
y               10         0

Now, we consider the point O(0, 0), i.e, origin.
Substitute in inequality x + 3y ≤ 30,  0 + 3(0) ≤ 30  or 0 ≤ 30 which is true. Therefore, we mark that region which contains origin.
Now, we shade the common region. The solution is given by the shaded portion OABC of the graph given below;