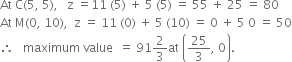We are to maximize
z = 11x + 5y
subject to the constraints
3x + 2y  ≤ 25
x + y ≤ 10
x ≥ 0, y ≥ 0.
Consider a set of rectangular cartesian axes OXY in the plane.
It is clear that any point which satisfies x ≥ 0, y ≥ 0 lies in the first quadrant.
Now we draw the graph of 3x + 2y = 25
For x = 0,   2y = 25   or   
For y = 0,  3x = 25   or   


Again we draw the graph of x + y = 10
For x = 0, y = 10
For y = 0, x = 10
∴  line meets OX in B (10, 0) and OY in M (0, 10).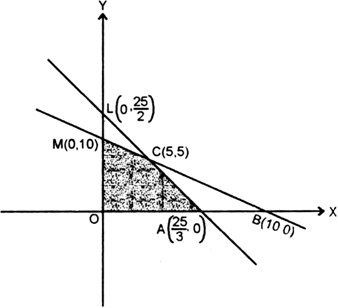

Since feasible region is the region which satisfies all the constraints
∴   OACM is the feasible region and corner points are

At  

At