Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Linear Programming

Long Answer Type

21.

Solve the following linear programming problem graphically:
Minimise Z = 3x + 2y
subject to the constraints x + y ≥ 8, 3x + 5 y ≤ 15, x ≥ 0, y ≥ 0

89 Views

22.

Solve the following linear programming problem graphically:
Minimise Z = x + y
subject to the constraints x - y ≤ - 1, - x + y ≤ 0, x, y ≥ 0.

85 Views

23. A furniture dealer deals in the sale of only tables and chairs. He has Rs. 5000 to invest and a space to store at most 60 pieces. A table costs him Rs. 250 and a chair Rs. 50. He can sell a table at a profit of Rs. 50 and a chair at a profit of Rs. 15. Assuming that he can sell all the items that he buys, how should he invest his money in order that he may maximise his profit?

153 Views

24. A cooperative society of farmers has 50 hectare of land to grow two crops X and Y. The profits from crops X and Y per hectare are estimated as Rs. 10,500 and Rs. 9,000 respectively. To control weeds, a liquid herbicide has to be used for crops X and Y at rates of 20 litres and 10 litres per hectare. Further, no more than 800 litres of herbicide should be used in order to protect fish and wild life using a pond which collects drainage from this land. How much land should be allocated to each crop so as to maximise the total profit of the society?

91 Views

25. A manufacturing company makes two models A and B of a product. Each piece of Model A requires 9 labour hours for fabricating and 1 labour hour for finishing. Each piece of Model B requires 12 labour hours for fabricating and 3 labour hours for finishing. For fabricating and finishing, the maximum labour hours available are 180 and 30 respectively. The company makes a profit of Rs. 8000 on each piece of model A and Rs. 12000 on each piece of Model B. How many pieces of Model A and Model B should be manufactured per week to realise a maximum profit? What is the maximum profit per week?

106 Views

26. One kind of cake requires 200g of flour and 25g of fat, and another kind of cake requires 100g of flour and 50g of fat. Find the maximum number of cakes which can be made from 5 kg of flour and 1 kg of fat assuming that there is no shortage of the other ingredients used in making the cakes.

95 Views

27.

A factory makes tennis rackets and cricket bats. A tennis racket takes 1.5 hours of machine time and 3 hours of craftman’s time in its making while a cricket bat takes 3 hours of machine time and 1 hour of craftman’s time. In a day, the factory has the availability of not more than 42 hours of machine time and 24 hours of craftman’s time.
(i) What number of rackets and bats must be made if the factory is to work at full capacity?
(ii) If the profit on a racket and on a bat is Rs 20 and Rs 10 respectively, find the maximum profit of the factory when it works at full capacity.

100 Views

28. A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs.17.50 per package on nuts and Rs. 7.00 per package on bolts. How many packages of cach should be produced each day as to maximise his profit, if he operates his machines for at the most 12 hours a day?

116 Views

29.

If a young man rides his motor - cycle at 25 km per hour, he has to spend Rs. 2 per km on petrol ; if he rides it at a faster speed of 40 km per hour, the petrol cost increases to Rs. 5 per km. He has Rs. 100 to spend on petrol and wishes to find what is the maximum distance he can travel within one hour. Express this as a linear programming problem and then solve it.

86 Views

30.
A firm is engaged in producing two products A and B. Each unit of product A requires two kg of raw material and four labour hours for processing whereas each unit of product B requires three kg of raw material and three hours of labour, of the same type. Every week, the firm has an availability of 60 kg of raw material and 96 labour hours. One unit of product A sold yields Rs. 40 and one unit of product B sold gives Rs. 35 as profit.
Formulate this problem as linear programming problem to determine as to how many units of each of the products should be produced per week so that the firm can earn the maximum profit. Assume that there is no marketing constraints so that all that is produced can be sold.

Let x and y represent the number of units produced per week of the products A and B respectively. Let Z be the profit corresponding to this rate of production. Then
Z = 40 x + 35 y ...(1)
In order to produce these number of units,
total consumption of raw material = 2x + 3y
and total labour hours needed = 4x + 3y
But total raw material available = 60 kg
and total labour hours available = 96
∴ we have,
$open table attributes columnalign right end attributes row cell 2 straight x plus 3 straight y space less or equal than 60 end cell row cell and space space 4 straight x plus 3 straight y less or equal than 96 end cell end table close curly brackets$ ...(2)
∵ it is not possible to produce negative number of units
∴ x ≥ 0, y ≥ 0 ...(3)
∴ firm’s allocation problem can be put in the following mathematical form:
Find two real numbers x and y such that
2x + 3y ≤ 60
4x + 3y ≤ 96
x ≥ 0, y ≥ 0
and for which the objective function
Z = 40x + 35y
is maximum
Consider a set of rectangular axes OXY in the plane.
It is clear that any point which satisfies x ≥ 0, y ≥ 0 lies in the first quadrant.
Let us draw the graph of
2x + 3y = 60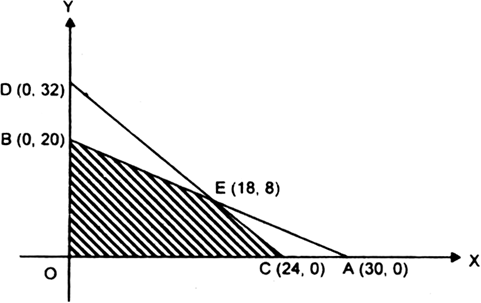

For x = 0, 3 y = 60 or y = 20
For y = 0, 2 x = 60 or x = 30
∴ line 2x + 3y = 60 meets OX in A (30, 0) and OY in B (0, 20).
Now we draw the graph of 4x + 3y = 96
For x = 0, 3y = 96 or y = 32
For y = 0, 4x = 96 or x = 24
∴ line 4x + 3y = 96 meets OX in C (24, 0) and OY in D (0, 32).
Since feasible region is the region which satisfies all the constraints.
∴ OCEB is the feasible region.
The corner points are O (0, 0), C (24, 0), E (18, 8), B (0, 20).
At O (0, 0), Z = 40 (0) 35 (0) = 0 + 0 = 0
At C (24, 0), Z = 40 (24) + 35 (0) = 960 + 0 = 960
At E (18, 8), Z = 40 (18)+ 35 (8) = 720 + 280 = 1000
At B(0, 20), Z = 40(0) + 35 (20) = 0 + 700 = 700
Here Rs. 1000 is the maximum values of Z and occurs at E (18, 8)
∴ optimal solution is x = 18, y = 8
i.e., 18 units of A and 8 units of B.

134 Views