Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Linear Programming

Multiple Choice Questions

41.

The corner points of the feasible region determined by the following system of linear inequalities:
2x + y ≤ 10, x + 3y ≤ 15, x, y ≥ 0 are (0, 0), (5, 0), (3, 4) and (0, 5). Let Z = px + qy, where p, q > 0. Condition on p and q so that the maximum of Z occurs at both (3, 4) and (0, 5) is

p = q
p = 2 q
p = 3 q
p = 3 q

102 Views

Long Answer Type

42.

A dietician has to develop a special diet using two foods P and Q. Each packet (containing 30 g) of food P contains 12 units of calcium, 4 units of iron, 6 units of cholesterol and 6 units of vitamin A. Each packet of the same quantity of food Q contains 3 units of calcium, 20 units of iron, 4 units of cholesterol and 3 units of vitamin A. The diet requires at least 240 units of calcium, at least 460 units of iron and at most 300 units of cholesterol. How many packets of each food should be used to minimise the amount of vitamin A in the diet? What is the minimum amount of vitamin A?
How many packets of each food should be used to maximise the amount of vitamin A in the diet? What is the maximum amount of vitamin A in the diet?

97 Views

43.
A manufacturer has three machines 1, II and III installed in his factory. Machines I and II are capable of being operated for at most 12 hours whereas machine III must be operated for at least 5 hours a day. She produces only two items M and N each requiring the use of all the three machines.
The number of hours required for producing 1 unit of each of M and N on the three machines are given in the following table:

Items

Number of 1

ours required

on machines

I

II

III

M

1

2

1

N

2

1

1.25

She makes a profit of Rs. 600 and Rs. 400 on items M and N respectively. How many of each item should she produce so as to maximise her profit assuming that she can sell all the items that she produced? What will be the maximum profit?

Let x and y be the number of items M and N respectively.
Total profit on the production = Rs. (600 x + 400 y)
Let Z be the profit.
Mathematical formulation of the given problem is as follows:
Maximise Z = 600 x + 400 y
subject to the constraints
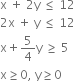
$straight x space plus space 2 straight y space less or equal than space 12 2 straight x space plus space straight y space less or equal than space 12 straight x plus 5 over 4 straight y space greater or equal than space 5 straight x greater or equal than 0 comma space straight y greater or equal than 0$

Consider a set of rectangular cartesian axes OXY in the plane.
It is clear that any point which satisfies x ≥ 0, y ≥ 0 lies in the first quadrant.
Now we draw the graph of x + 2y = 12
For x = 0, 2 y = 12 or y = 6
For y = 0, x = 12
∴ line meets OX in A(12, 0) and OY in L(0, 6).
Also we draw the graph of 2x + y = 12
For x = 0, y = 12
For y = 0, 2x = 12 or x = 6
∴ line meets OX in B(6, 0) and OY in M(0, 12).
Again we draw the graph of
$straight x plus 5 over 4 straight y space equals space 5$
For x = 0, $5 over 4 straight y space equals space 5 space space or space space straight y space equals space 4$
For y = 0, x = 5
∴ line meets OX in C(5, 0) and OY in N(0, 4).
Since feasible region satisfies all the constraints.
∴ CBDLN is the feasible region.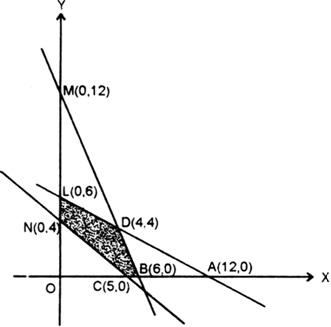

The corner points are C(5, 0), B(6, 0),
D(4, 4), L(0, 6), N(0, 4).
At C(5, 0), Z = 600 × 5 + 400 × 0 = 3000 + 0 = 3000
At B(6, 0), Z = 600 × 6 + 400 × 0 = 3600 + 0 = 3600
At D(4, 4), Z = 600 × 4 + 400 × 4 = 2400 + 1600 = 4000
At L(0, 6), Z = 600 × 0 + 400 × 6 = 0 + 2400 = 2400
At N(0, 4), Z = 600 × Ot 400 × 4 = 0 + 1600 = 1600
∴ maximum value = 4000 at (4, 4).
∴ manufacturer has to produce 4 units of each item to get the maximum profit of Rs. 4000.

101 Views

44.

A manufacturer makes two types of toys A and B. Three machines are needed for this purpose and the time (in minutes) requires for each toy on the machines is given below:

Types of Toys		Machines
	I	II	III
A	12	18	6
B	6	0	9

Each machine is available for a maximum of 6 hours per day. If the profit on each toy of type A is Rs. 7.50 and that on each toy of type B is Rs. 5, show that 15 toys of type A and 30 of type B should be manufactured in a day to get maximum profit.

128 Views

45.

Two godowns A and B have grain capacity of 100 quintals and 50 quintals respectively. They supply to 3 ration shops, D, E and F whose requirements arc 60, 50 and 40 quintals respectively. The cost of transportation per quintal from the godowns to the shops arc given in the following table:

Transportation cost per quintal (in Rs.)
From/To	A	B
D	6	4
E	3	2
F	2.50	3

How should the supplies be transported in order that the transportation cost is minimum ? What is the minimum cost?

91 Views

46.

A fruit grower can use two types of fertilizer in his garden, brand P and brand Q. The amounts (in kg.) of nitrogen, phosphoric acid, potash, and chlorine in a bag of each brand are given in the table. Tests indicate that the garden needs at least 240 kg of phosphoric acid, at least 270 kg. of potash and at most 310 kg. of chlorine.
If the grower wants to minimise the amount of nitrogen added to the garden, how many bags of each brand should be used? What is the minimum amount of nitrogen added in the garden?

	kg. per bag
	Brand P	Brand Q
Nitrogen	3	3.5
Phosphoric acid	1	2
Potash	3	1.5
Chlorine	1.5	2

If the grower wants to maximise the amount of nitrogen added in the garden, how many bags of each brand should be added? What is the maximum amount of nitrogen added?

84 Views

47. A toy company manufactures two types of dolls, A and B. Market tests and available resources have indicated that the combined production level should not exceed 1200 dolls per week and the demand for dolls of type B is at most half of that for dolls of type A. Further, the production level of dolls of type A can exceed three times the production of dolls of other type by at most 600 units. If the company makes profit of Rs.12 and Rs. 16 per doll respectively on dolls A and B, how many of each should be produced weekly in order to maximise the profit?

113 Views

48. An aeroplane can carry a maximum of 200 passengers. A profit of Rs 1000 is made on each executive class ticket and a profit of Rs. 600 is made on each economy class ticket. The airline reserves at least 20 seats for executive class. However, at least 4 times as many passengers prefer to travel by economy class than by the executive class. Determine how many tickets of each type must be sold in order to maximise the profit for the airline. What is the maximum profit?

132 Views

49.

There are two factories located one at place P and the other at place Q. From these locations, a certain commodity is to be delivered to each of the three depots situated at A, B and C. The weekly requirements of the depots are respectively 5, 5 and 4 units of the commodity while the production capacity of the factories at P and Q are respectively 8 and 6 units The cost of transportation per unit is given below:

From/To		Cost (in Rs.)
	A	B	C
P	160	100	150
Q	100	120	100

How many units should be transported from each factory to each depot in order that the transportation cost is minimum. What will be the minimum transportation cost?

223 Views

50.

An oil company has two depots A and B with capacities of 7000 L and 4000 L respectively. The company is to supply oil to three petrol pumps, D. E and F whose requirements are 4500 L, 3000 L and 3500 L respectively. The distance (in km.) between the depots and the petrol pumps are given in the following table:

	Distance (in km.)
From/To	A	B
D	7	3
E	6	4
F	3	2

Assuming that the transportation cost of 10 litres of oil is Re 1 per km., how should the delivery be scheduled in order that the transportation cost is minimum? What is the minimum cost?

100 Views