 Multiple Choice Questions
Multiple Choice QuestionsThe maximum value of = 3x + 4y, subject to the conditions x + y 40, x + 2y 60, x, y 0, is
130
140
40
120
If x + y 2; x 20, y 20, then the point, at which the maximumvalue of 3x + 2y is attained, will be
(0, 0)
(2, 0)
(0, 2)
The maximum value of P = 6x + 8y, if 2x + y 30, x + 2y 24; x 20, y 20, will be
90
120
96
240
B.
120
Given, inequalities are
2x + y 30, x + 2y 5; 24, x 0, y 0
Given, P = 6x + 8y
Here, feasible region is OABCO
At O(0, 0), P = 6(0) + 8(0) = 0
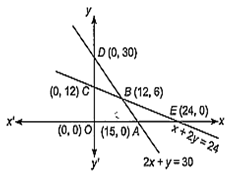
At A(15, 0), P = 6(15) + 8(0)= 90
At B(12, 6), P = 6(12) + 8(6) = 120
At C(0, 12), P = 60)+ 8(12) = 96
Hence, maximum value of P is 120.
Regression of saving (s) of a family on income y may be expressed as s = a + , where a and m are constants. In a random sample of 100 families the variance of savings is one quarter of the variance of incomes and the correlation coefficient is found to be 0.8, the value of m is
0.8
1.25
0.25
None of these
