Short Answer Type
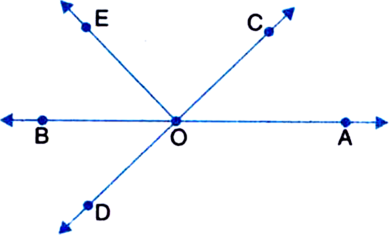
Short Answer TypeRays OA, OB. OC, OD and OE have the common initial point O. Show that ∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360°.

This leads to two pairs of vertically opposite angles, namely,
(i) ∠AOC and ∠BOD
(ii) ∠AOD and ∠BOC
We are to prove that
(i) ∠AOC = ∠BOD
and (ii) ∠AOD = ∠BOC
∵ Ray OA stands on line CD Therefore,
∠AOC + ∠AOD = 180° ...(1)
| Linear Pair Axiom
∵ Ray OD stands on line AB Therefore,
∠AOD + ∠BOD = 180° ...(2)
| Linear Pair Axiom
From (1) and (2),
∠AOC + ∠AOD = ∠AOD + ∠BOD
⇒ ∠AOC = ∠BOD
Similarly, we can prove that
∠AOD = ∠BOC