Short Answer Type
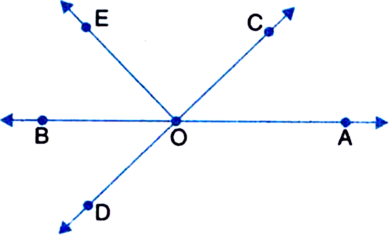
Short Answer TypeRays OA, OB. OC, OD and OE have the common initial point O. Show that ∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360°.

Given: OP bisects ∠AOC, OQ bisects ∠BOC and OP ⊥ OQ.
To Prove: The points A, O and B are collinear.
Proof: ∵ OP bisects ∠AOC
∴ ∠AOP = ∠COP ...(1)
∵ OQ bisects ∠BOC
∠BOQ = ∠COQ ...(2)
Now, ∠AOB
= ∠AOP + ∠COP + ∠COQ + ∠BOQ
= ∠COP + ∠COP + ∠COQ + ∠COQ
| From (1) and (2)
= 2(∠COP + ∠COQ)
= 2 ∠POQ
= 2(90°) | ∵ OP ⊥ OQ
= 180°
∴ The points A, O and B are collinear.
| By converse of Linear Pair Axiom