Short Answer Type
Short Answer TypeIn figure, if PQ || ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS.
[Hint. Draw a line parallel to ST through point R.]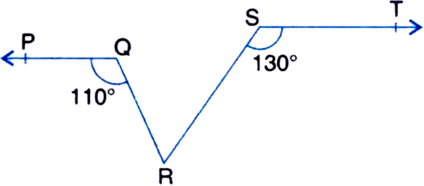
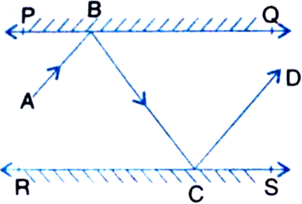
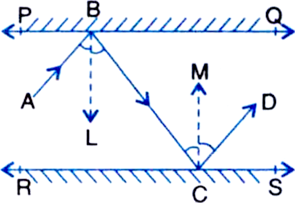
Proof: ∵ BL ⊥ PQ, CM ⊥ RS and PQ || RS ∴ BL || CM
∠LBC = ∠MCB ...(1)
| Alternate Interior Angles
∠ABL = ∠LBC ...(2)
| ∵ Angle of incidence = Angle of reflection
∠MCB = ∠MCD ...(3)
| ∵ Angle of incidence = Angle of reflection
From (1), (2) and (3), we get
∠ABL = ∠MCD ...(4)
Adding (1) and (4), we get
∠LBC + ∠ABL = ∠MCB + ∠MCD
⇒ ∠ABC = ∠BCD
But these are alternate interior angles and they are equal.
So, AB || CD.
In figure, EF is a transversal to two parallel lines AB and CD, GM and HL are the bisectors of the corresponding angles EGB and EHD. Prove that GM || HL.
[Hint. First prove that ∠EGM = ∠GHL]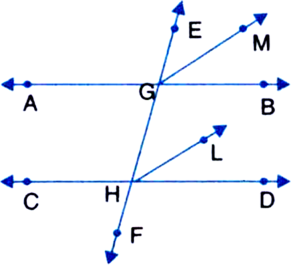
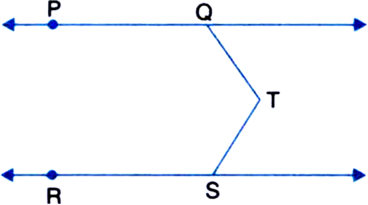
In figure, PQ || RS and T is any point as shown in the figure then show that
∠PQT + ∠QTS + ∠RST = 360°.