Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Lines and Angles

Short Answer Type

31.

In figure, if PQ || ST, ∠PQR = 110° and ∠RST = 130°, find ∠QRS.
[Hint. Draw a line parallel to ST through point R.]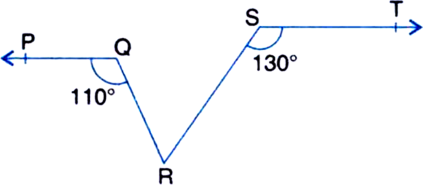

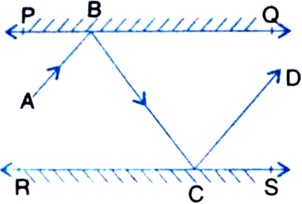
363 Views

32. In figure, if AB II CD, ∠APQ = 50° and ∠PRD = 127°, find x and y.

187 Views

33. In figure, PQ and RS are two mirrors placed parallel to each other. An incident ray AB strikes the mirror PQ at B, the reflected ray moves along the path BC and strikes the mirror RS at C and again reflects back along CD. Prove that AB || CD.

251 Views

34.

In figure, if x = y and a = b, prove that r || n.

293 Views

35. If two lines are perpendicular to the same line, prove that they are parallel to each other.

427 Views

36.

In figure, EF is a transversal to two parallel lines AB and CD, GM and HL are the bisectors of the corresponding angles EGB and EHD. Prove that GM || HL.

[Hint. First prove that ∠EGM = ∠GHL]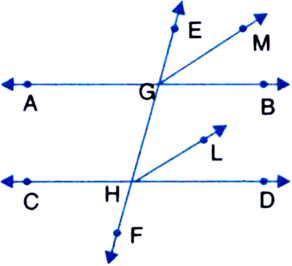

461 Views

37. In figure, if AB || CD then find the value of y.

371 Views

38. In figure, is line I parallel to m? Justify your answer.

622 Views

39.
In figure, PQ || RS and T is any point as shown in the figure then show that

∠PQT + ∠QTS + ∠RST = 360°.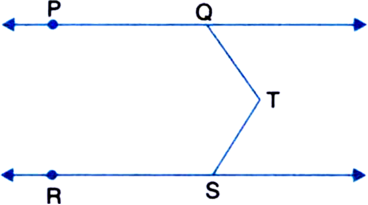

Given: PQ || RS and T is any point.
To Prove: ∠PQT + ∠QTS + ∠RST = 360°
Construction: Through T, draw TU || PQ || RS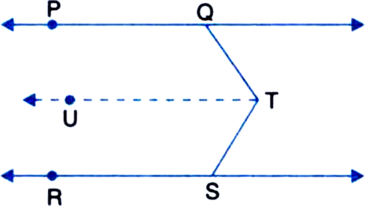

Proof: ∵ PQ || UT | By construction and a transversal QT intersects then
∴ ∠PQT + ∠QTU = 180°    ...(1)
| Sum of consecutive interior angles on the same sides of a transversal is 180°
∵ UT || RS    | By construction and a transversal TS intersects them
∴ ∠UTS + ∠RST = 180°    ...(2)
| Sum of consecutive interior angles on the same side of a transversal is 180°
Adding (1) and (2), we get
∠PQT + (∠QTU + ∠UTS) + ∠RST = 360°
⇒     ∠PQT + ∠QTS + ∠RST = 360°

607 Views