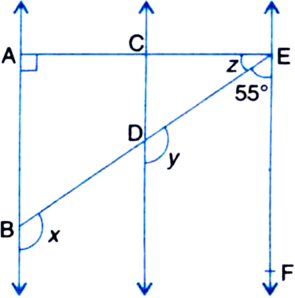
Short Answer Type
Short Answer Type Long Answer Type
Long Answer TypeGiven: Two parallel lines AB and CD are intersected by a transversal EF in points G and H respectively. The bisectors of two pairs of interior angles intersect in L and M.
To Prove: GLHM is a rectangle.
Proof: ∵ AB || CD and a transversal EF intersects them![]()
| Alternate interior angles![]()
| Halves of equals are equal![]()
But these form a pair of equal alternate interior angles
∴ GM || HL ...(1)
Similarly, we can show that
HM || GL ...(2)
In view of (1) and (2),
GLHM is a parallelogram
| A quadrilateral is a parallelogram if its both the pairs of opposite sides are parallel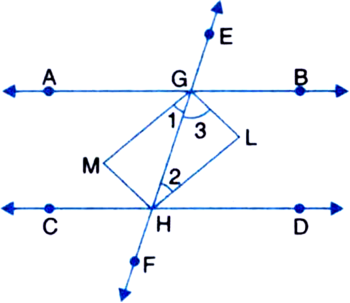
Now, since the sum the consecutive interior angles on the same side of a transversal is 180°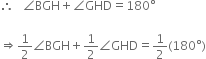
| Halves of equals are equal
⇒ ∠3 + ∠2 = 90° ...(3)
In ∆GHL,
∠3 + ∠2 + ∠GLH = 180°
| Angle sum property of a triangle
⇒ 90° + ∠GLH = 180°
| From (3)
∠GLH = 90°
⇒ GLHM is a rectangle
| A parallelogram with one of its angles of measure 90° is a rectangle.
 Short Answer Type
Short Answer Type