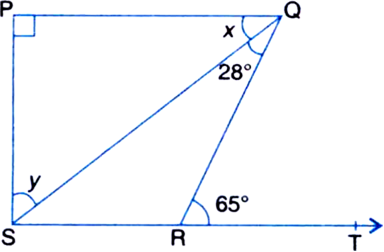
Short Answer Type
Short Answer Type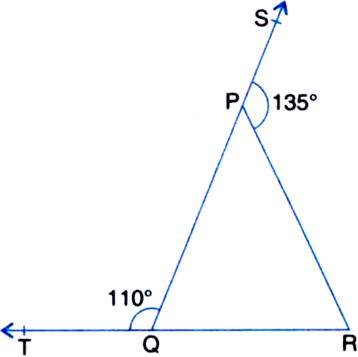
∵ TR is a line
∴ ∠PQT + ∠PQR = 180°
⇒ 110° + ∠PQR = 180°
⇒ ∠PQR = 180° - 110° = 70° ...(1)
∵ QS is a line
∴ ∠SPR + ∠QPR = 180°
⇒ 135° + ∠QPR = 180°
⇒ ∠QPR = 180° - 135° = 45° ...(2)
In ∆PQR,
∠PQR + ∠QPR + ∠PRQ = 180°
| ∵ The sum of all the angles of a triangle is 180°
⇒ 70° + 45° + ∠PRQ = 180°
| Using (1) and (2)
⇒ 115° + ∠PRQ = 180°
⇒ ∠PRQ = 180° - 115° = 65°.
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer TypeThe side EF, FD and DE of a triangle DEF are produced in order forming three exterior angles DFP, EDQ and FER respectively. Prove that
∠DFP + ∠EDQ + ∠FER = 360°.
OR
Prove that the sum of the exterior angles of a triangl is 360°.