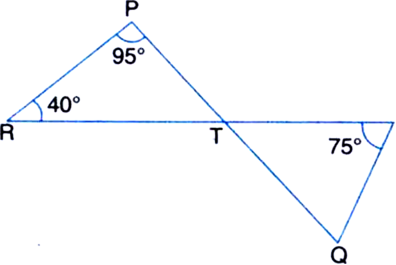
Short Answer Type
Short Answer Type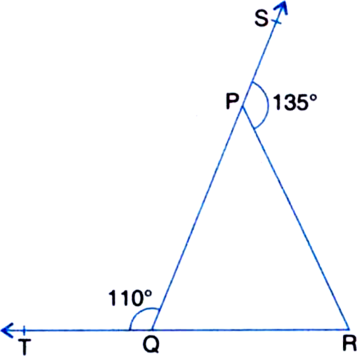
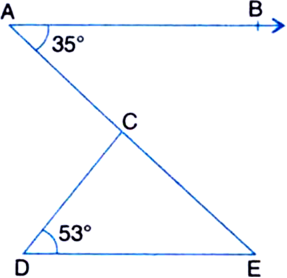
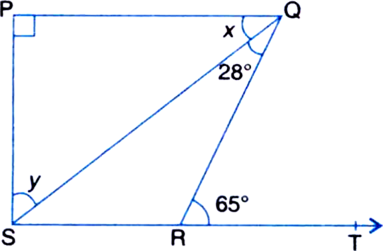
∠DEC = ∠BAC = 35° ...(1)
| Alternate Interior Angles
∠CDE = 53° ...(2) | Given
In ∆CDE,
∠CDE + ∠DEC + ∠DCE = 180°
| ∵ The sum of all the angles of a triangle is 180°.
⇒ 53°+ 35° + ∠DCE = 180°
| Using (1) and (2)
⇒ 88° + ∠DCE = 180°
⇒ ∠DCE = 180° - 88° = 92°.
 Long Answer Type
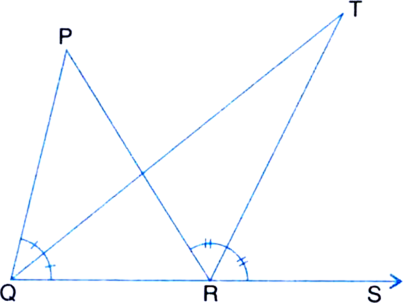
Long Answer Type Short Answer Type
Short Answer TypeThe side EF, FD and DE of a triangle DEF are produced in order forming three exterior angles DFP, EDQ and FER respectively. Prove that
∠DFP + ∠EDQ + ∠FER = 360°.
OR
Prove that the sum of the exterior angles of a triangl is 360°.