Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Lines and Angles

Short Answer Type

61. In figure, sides QP and RQ of ∆PQR are produced to points S and T respectively. If ∠SPR = 135° and ∠PQT = 110°. find ∠PRQ.

549 Views

62. In figure, ∠X = 62°, ∠XYZ = 54°. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ∆XYZ, find ∠OZY and ∠YOZ.

1694 Views

63. In figure, if AB || DE, ∠BAC = 35° and ∠CDE = 53°, find ∠DCE.

555 Views

64. In figure, if lines PQ and RS intersect at point T, such that ∠PRT = 40°, ∠RPT = 95° and ∠TSQ = 75°, find ∠SQT.

431 Views

65. In figure, if PQ ⊥ PS, PQ || SR, ∠SQR = 28° and ∠QRT = 65°, then find the values of x and y.

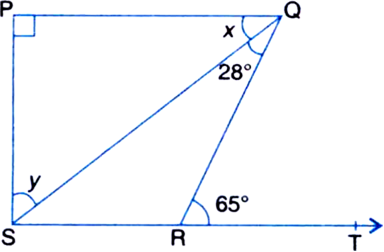
∠QRT = ∠RQS + ∠QSR
| ∵ The exterior angle is equal to the sum of the two interior opposite angles. ⇒    65°
= 28° + ∠QSR
⇒ ∠QSR = 65° - 28° = 37°
∵ PQ ≠ SP
∴ ∠QPS = 90°
∵ PQ || SR
∴ ∠QPS + ∠PSR = 180°
| ∵ The sum of consecutive interior angles on the same side of the transversal is 180°
⇒ 90° + ∠PSR = 180°
⇒    ∠PSR = 180° - 90° = 90°
⇒ ∠PSQ + ∠QSR = 90°
⇒    y + 37° = 90°
⇒    y = 90° - 37° = 53°
In ∆PQS,
∠PQS + ∠QSP + ∠QPS = 180°
| ∵ The sum of all the angles of a triangle is 180°
⇒ x + y + 90° = 180°
⇒ x + 53° + 90° = 180°
⇒    x + 143° = 180°
⇒ x = 180° - 143° = 37°.

380 Views

66. In figure, the side QR of ∆PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that

angle QTR equals 1 half angle QPR

258 Views

67. Prove that if one angle of a triangle is equal to the sum of the other two angles, the triangle is right angled.

102 Views

Long Answer Type

68. In figure, the bisectors of ∠ABC and ∠BCA intersect each other at the point O. Prove that

angle BOC equals 90 degree plus 1 half angle straight A

1125 Views

Short Answer Type

69.

The side EF, FD and DE of a triangle DEF are produced in order forming three exterior angles DFP, EDQ and FER respectively. Prove that
∠DFP + ∠EDQ + ∠FER = 360°.

Prove that the sum of the exterior angles of a triangl is 360°.

855 Views

70. In the figure, AD and CE are the angle bisectors of ∠A and ∠C respectively. If ∠ABC = 90° then find ∠AOC.

812 Views