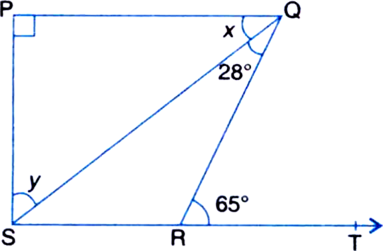
Short Answer Type
Short Answer Type
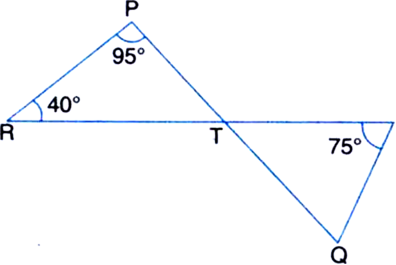
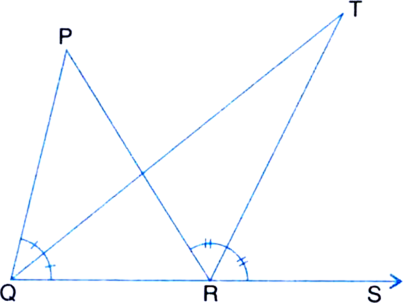
∵ ∠TRS is an exterior angle of ∆TQR ∴ ∠TRS = ∠TQR + ∠QTR ...(1)
| ∵ The exterior angle is equal to sum of its two interior opposite angles
∵ ∠ PRS is an exterior angle of ∆PQR
∴ ∠PRS = ∠PQR + ∠QPR ...(2)
| ∵ The exterior angle is equal to the sum of its two interior opposite angles
⇒ 2 ∠TRS = 2∠TQR + ∠QPR
| ∵ QT is the bisector of ∠PQR and RT is the bisector of ∠PRS
⇒ 2(∠TRS - ∠TQR) = ∠QPR ...(3)
From (1),
∠TRS - ∠TQR = ∠QTR ...(4)
From (3) and (4), we obtain
![]()
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer TypeThe side EF, FD and DE of a triangle DEF are produced in order forming three exterior angles DFP, EDQ and FER respectively. Prove that
∠DFP + ∠EDQ + ∠FER = 360°.
OR
Prove that the sum of the exterior angles of a triangl is 360°.