Short Answer Type
Short Answer Type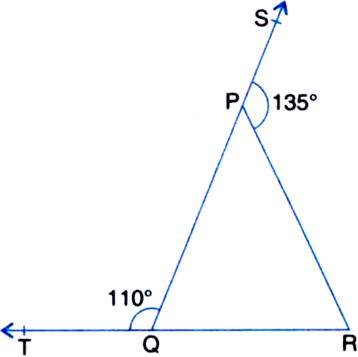
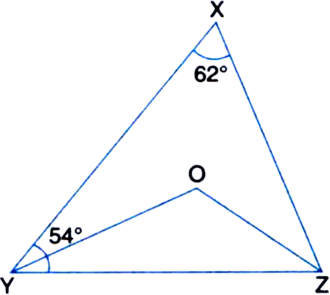
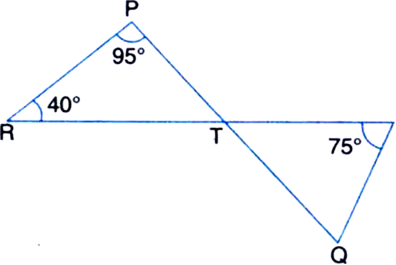
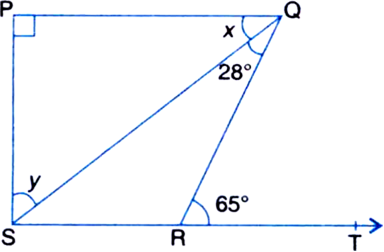
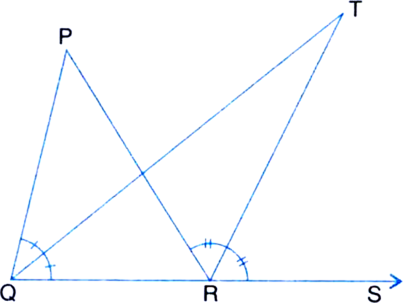
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer TypeThe side EF, FD and DE of a triangle DEF are produced in order forming three exterior angles DFP, EDQ and FER respectively. Prove that
∠DFP + ∠EDQ + ∠FER = 360°.
OR
Prove that the sum of the exterior angles of a triangl is 360°.
∠DFP = ∠D + ∠E ...(1)
| Exterior Angle Theorem
∠EDQ = ∠E + ∠F ...(2)
| Exterior Angle Theorem
∠FER = ∠F + ∠D ...(3)
| Exterior Angle Theorem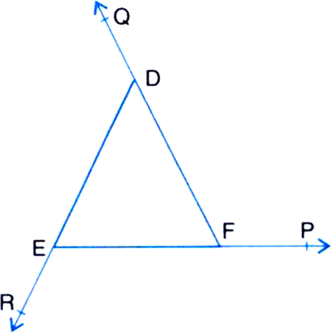
Adding (1), (2) and (3), we get
∠DFP + ∠EDQ + ∠FER = 2(∠D + ∠E + ∠F)
But ∠D + ∠E + ∠F = 180°
| ∵ The sum of the three angles of a triangle is 180°
∴ ∠DFP + ∠EDQ + ∠FER = 2(180°) = 360°.