Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Lines and Angles

Short Answer Type

71. In figure, find the value of x.

140 Views

72. In figure, if QT ⊥ PR, ∠TQR = 40° and ∠SPR = 30°, find the value of x and y.

183 Views

73. In figure, if line segment AB intersects CD at O such that ∠OAD = 80°, ∠ODA = 50° and ∠OCB = 40°, then find ∠OBC.

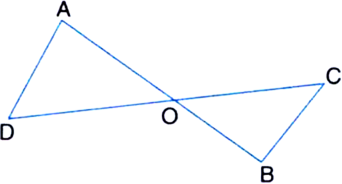
In ∆OAD,
∠OAD + ∠ODA + ∠AOD = 180°
| Angle sum property of a triangle
⇒ 80° + 50° + ∠AOD = 180°
⇒    130° + ∠AOD = 180°
⇒ ∠AOD = 180° - 130° = 50°
⇒ ∠BOC = 50°
| ∵ ∠AOD = ∠BOC (Vertically opposite angles)
In ∆OBC,
∠BOC + ∠OCB + ∠OBC = 180°
| Angle sum property of a triangle ⇒ 50° + 40° + ∠OBC = 180°
⇒     90° + ∠OBC = 180°
∠    ∠OBC = 180° - 90° = 90°

268 Views