 Short Answer Type
Short Answer Type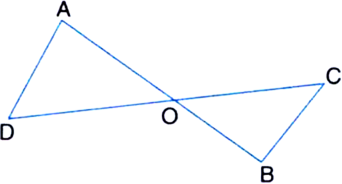
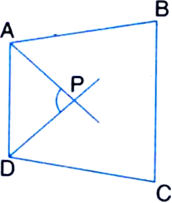
Given: AP and DP are bisectors of two adjacent angles A and D of a quadrilateral ABCD.
To Prove: 2 ∠APD = ∠B + ∠C
Proof: We know that the sum of all the angles of a quadrilateral is 360°. So,
∠A + ∠B + ∠C + ∠D = 360°
⇒ ∠A + ∠D = 360° - (∠B + ∠C) ...(1)
Now, in ∆PAD,
∠APD + ∠PAD + ∠PDA = 180°
| Angle sum property of a triangle![]()
∵ AP and DP are the bisectors of two adjacent angles A and D of quadrilateral ABCD
⇒ 2 ∠APD + ∠A + ∠D = 360°
⇒ 2 ∠APD = 360° - (∠A + ∠D)
⇒ 2∠APD = ∠B + ∠C
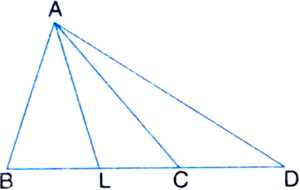
 Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type